5.4. Ponto em Polígono (PIP)
Uma das operações mais comuns em aplicações geoespaciais é determinar se um ponto encontra-se no interior de um polígono. Nesta seção vamos apresentar dois algoritmos para essa finalidade, que são comumente empregados nos sistemas geoespaciais.
5.4.1. Teste de Cruzamentos (Crossing Test)
No caso de polígonos simples (convexos ou não-convexos) podemos saber se um ponto encontra-se ou não no seu interior, traçando uma semi-reta horizontal (ou vertical) partindo desse ponto. Se esse raio cruzar um número ímpar de segmentos da fronteira do polígono, então este ponto encontra-se em seu interior, caso contrário, com um número par de cruzamentos, o ponto encontra-se fora do polígono. Podemos observar essa propriedade na Figura 5.7. Repare que as semi-retas horizontais partindo dos pontos \(P_3\) e \(P_4\), ambos no interior do polígono, cruzam os segmentos desse polígono um número ímpar de vezes. Já as semi-retas horizontais partindo dos pontos \(P_1\), \(P_2\), \(P_5\), \(P_6\) e \(P_7\), todos externos, cruzam os segmentos desse polígono um número par de vezes.
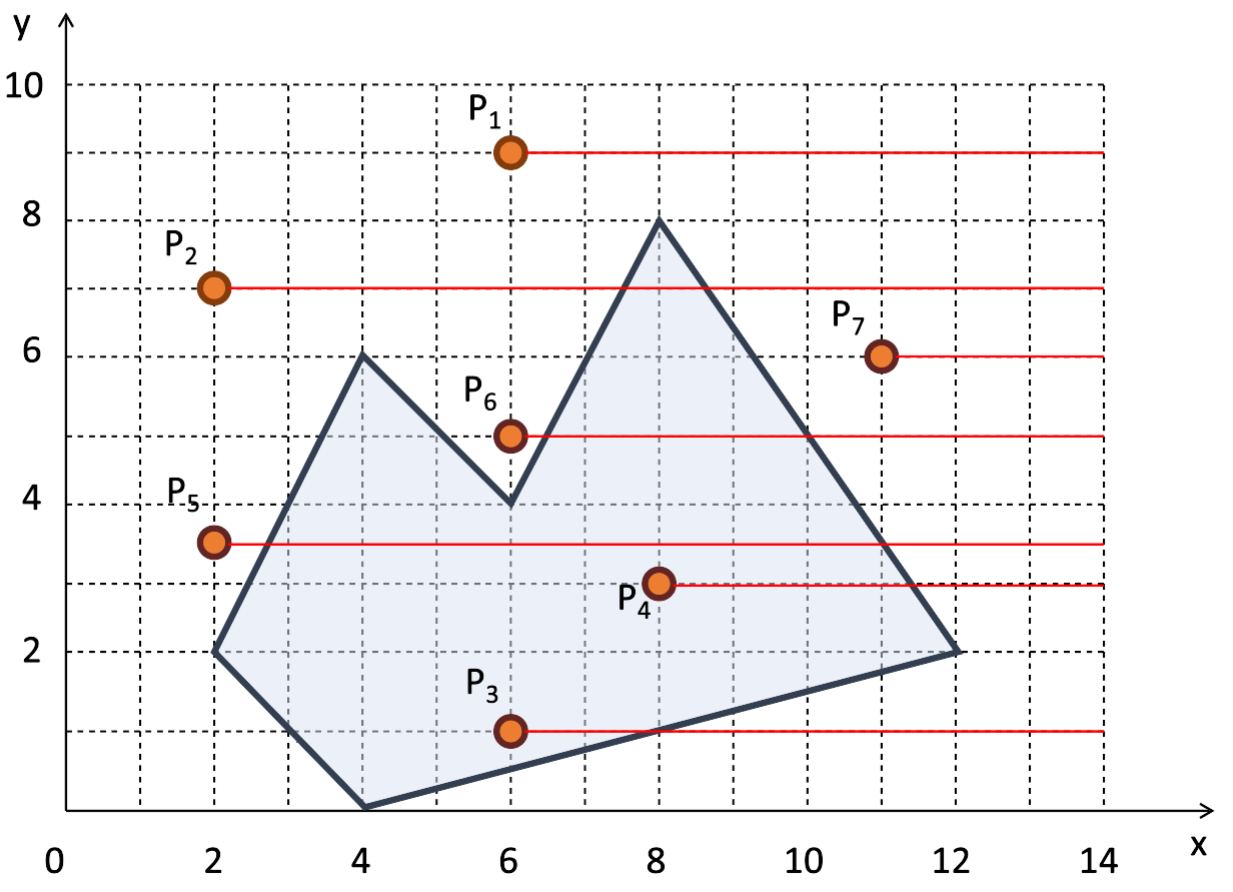
Figura 5.7 - Teste de cruzamento do raio horizontal
Esse algoritmo precisa tratar alguns casos especiais, mostrados nas Figuras 5.8, 5.9 e 5.10. Para saber detalhes de como esses casos são tratados, consulte o artigo online de Eric Haines.
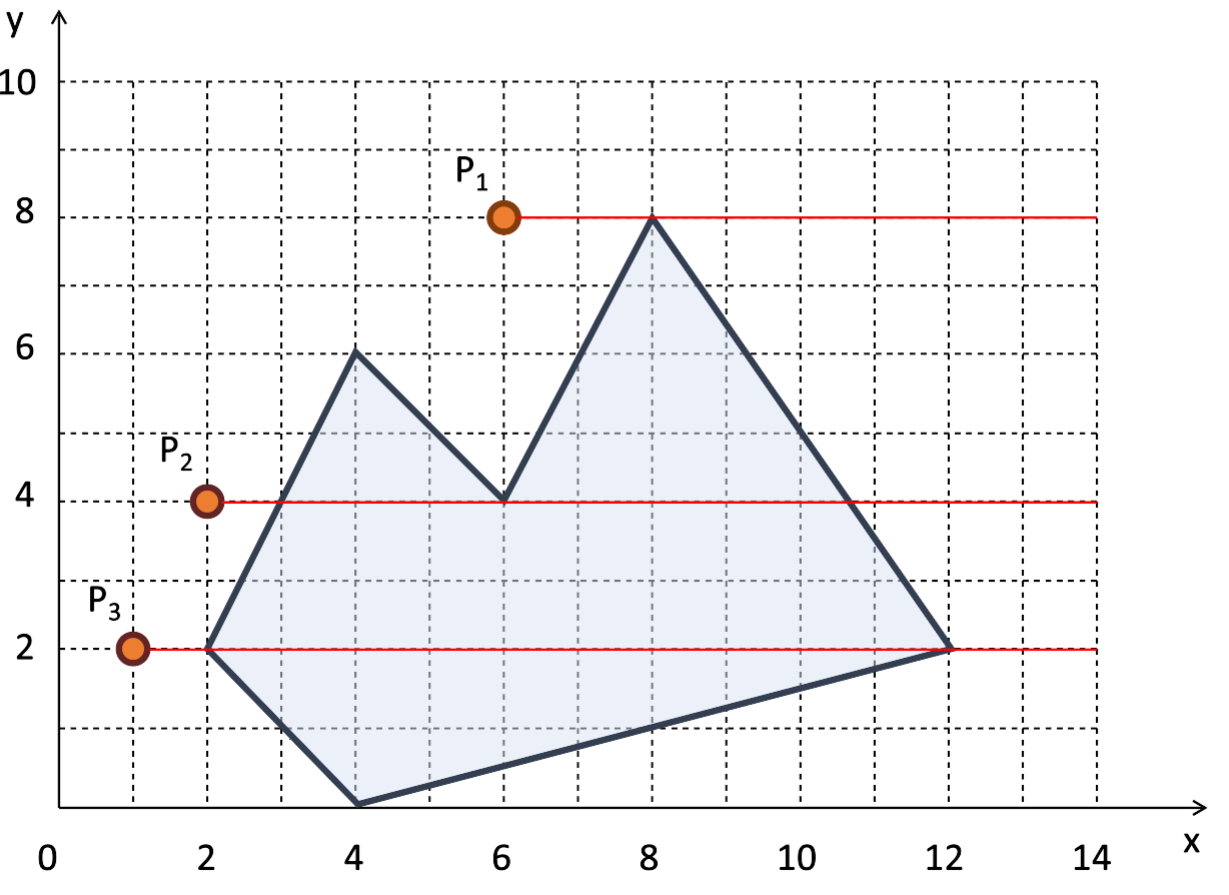
Figura 5.8 - Teste de cruzamento do raio horizontal
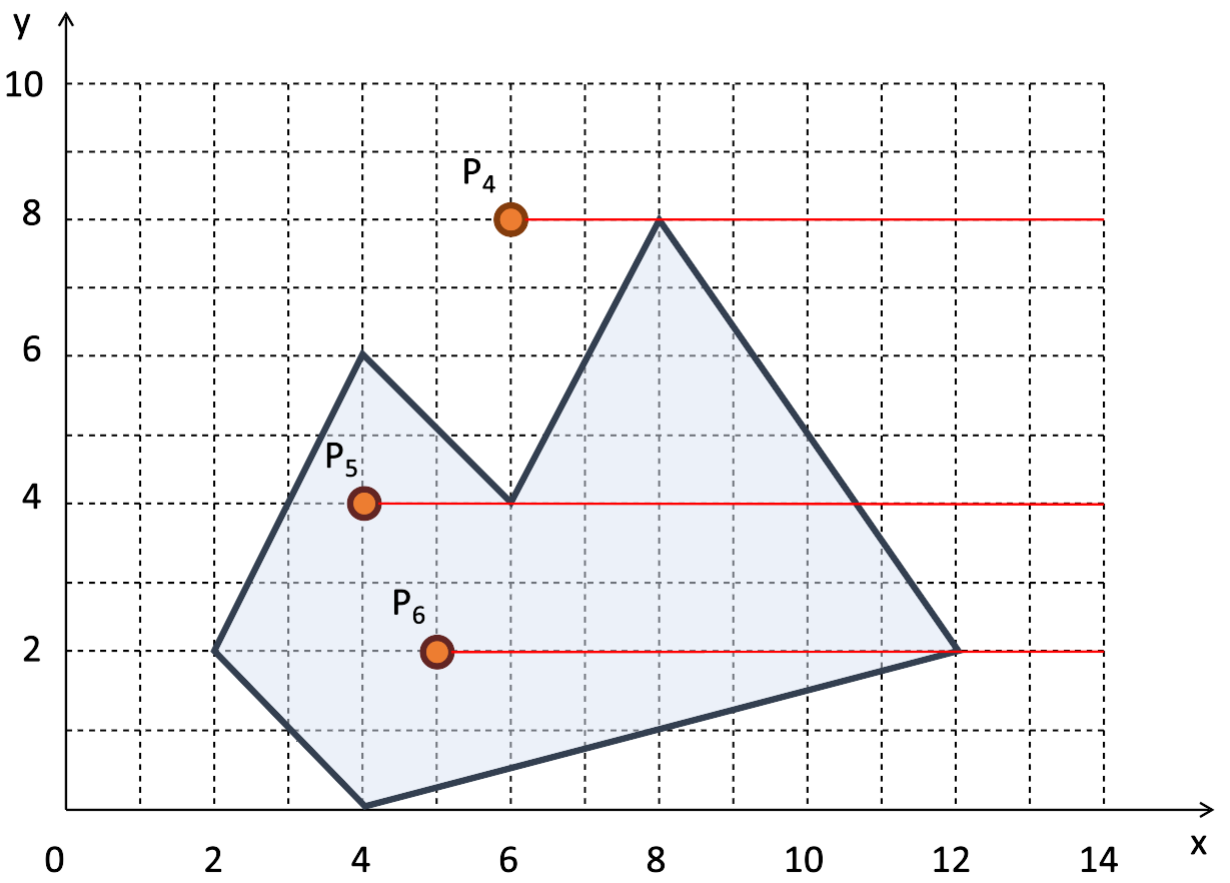
Figura 5.9 - Teste de cruzamento do raio horizontal
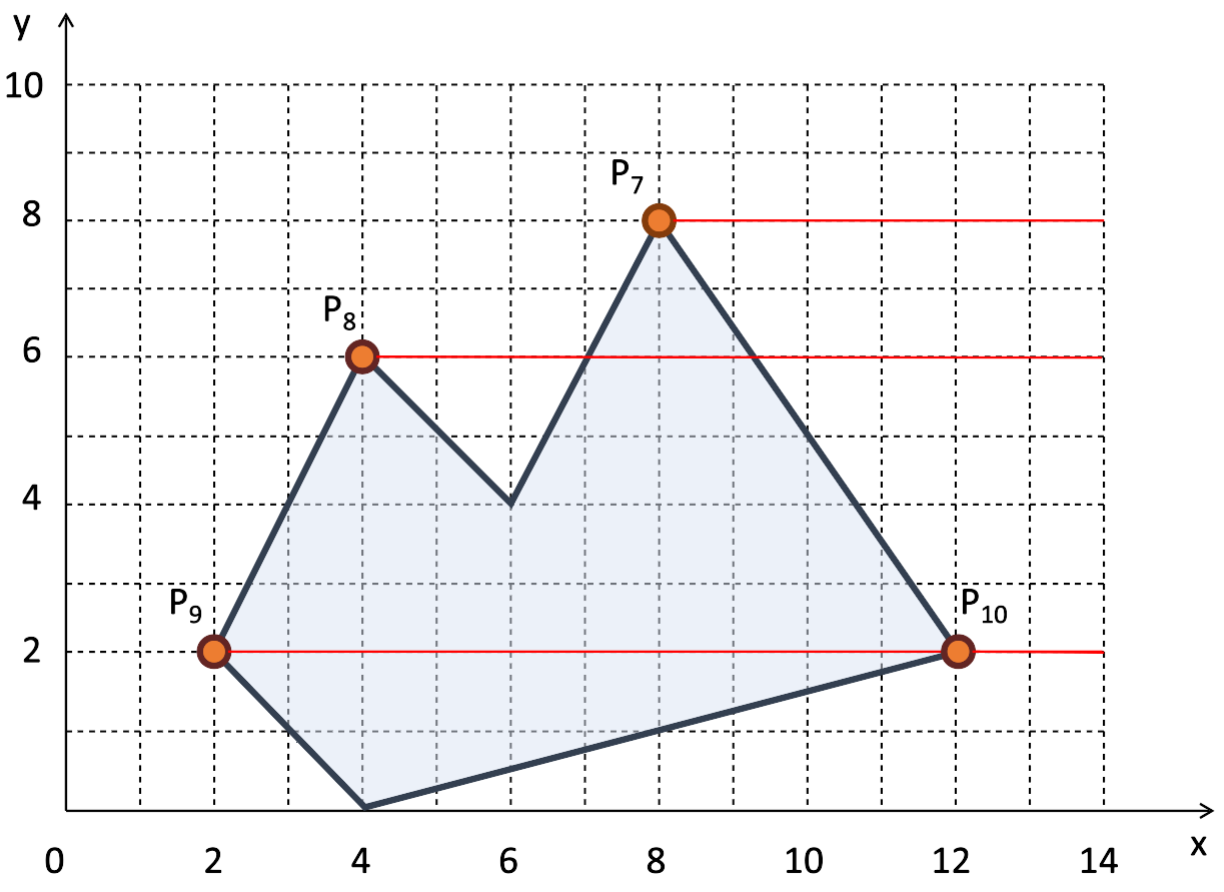
Figura 5.10 - Teste de cruzamento do raio horizontal
5.4.2. Usando Partições
Uma forma de acelerar a consulta de vários pontos ao mesmo polígono, consiste em utilizar uma estrutura de dados auxiliar construída como uma etapa de pré-processamento. A Figura 5.11 mostra como isso poderia ser feito com um vetor unidimensional onde cada entrada estaria associada aos segmentos de uma determinada faixa horizontal (bin). Dessa forma, ao testar um ponto, basta determinar a partição em que ele se encontra e então testar os segmentos associados a essa partição contando os cruzamentos. Como cada partição terá um número menor de segmentos do que o polígono como um todo, a tendência é diminuir a quantidade de testes de cruzamento realizados para cada ponto.
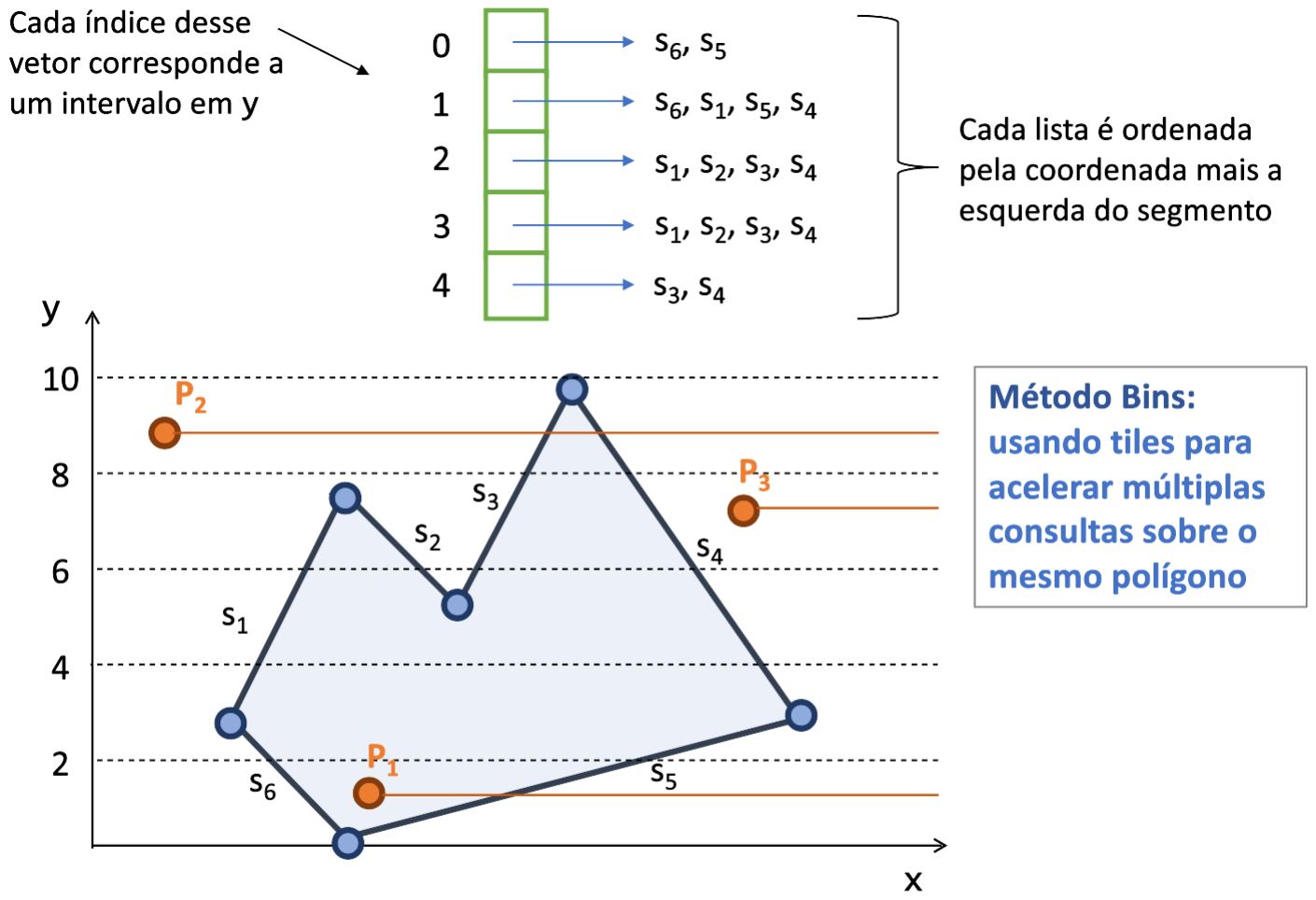
Figura 5.11 - Teste de cruzamento usando partições