7.6. Exercícios

Aviso

  • Os exercícios práticos devem ser desenvolvidos em PL/pgSQL ou PL/Python.

  • Escreva a documentação que achar pertinente dentro do próprio código fonte, que deverá utilizar a codificação de caracteres UTF-8.

  • A solução de cada exercício deverá ser entregue em arquivos de código fonte com a extensão .sql.

  • Envie por e-mail um único arquivo no formato zip, chamado lista-01.zip, contendo todos os arquivos de código fonte dos exercícios.

  • O título (assunto) do e-mail deve seguir o seguinte padrão: [geoinformatica-2023][lista-01] nome-aluno. Exemplo: [geoinformatica-2023][lista-01] gilberto.

  • Não use acentos ou caracteres especiais nos nomes dos arquivos ou no título do e-mail.

  • Prazo para entrega: 22/06/2023 - 18:00

Exercício 01. A fórmula de Haversine possbilita o cálculo de distâncias entre dois pontos em uma esfera a partir de suas latitudes e longitudes. Dada a seguinte fórmula:

(7.1)\[d(p, q) = 2r \arcsin{\sqrt{\sin^2({\frac{\phi_2 - \phi_1}{2}}) + \cos{\phi_1} \cos{\phi_2} \sin^2({\frac{\lambda_2 - \lambda_1}{2}})}}\]

onde:

  • \(r\): é o raio da esfera (\(\sim6371 km\)).

  • \(\phi_1\) e \(\phi_2\): latitude dos pontos em radianos.

  • \(\lambda_1\) e \(\lambda_2\): longitude dos pontos em radianos.

Construa uma função chamada DistanciaHaversine que receba como argumentos duas geometrias do tipo Point, representando duas localizações quaisquer em grau-decimal, e que retorne um único valor com a distância em km. Para maiores detalhes sobre essa fórmula, consulte a Wikipedia.

Aviso

O código fonte desse exercício deverá estar em dois arquivos: um contendo a definição da função, com o nome ex-01-haversine-ddl.sql, e outro com um exemplo de uso da função, chamado ex-01-haversine-dml.sql.

Exercício 02. Escreva uma função que calcule a menor distância entre um ponto \(P\) qualquer e uma reta \(r\) qualquer (Figura 7.14). Os parâmetros desta função deverão utilizar o tipo PostGIS Geometry, com o ponto representado por um elemento geométrico do tipo Point e a reta, por um LineString contendo dois pontos da reta.

Nota

A menor distância entre um ponto \(P\) e uma reta \(r\) corresponde ao segmento de reta perpendicular a \(r\) que parte de \(P\) e chega a \(r\), como ilustrado na Figura 7.14.

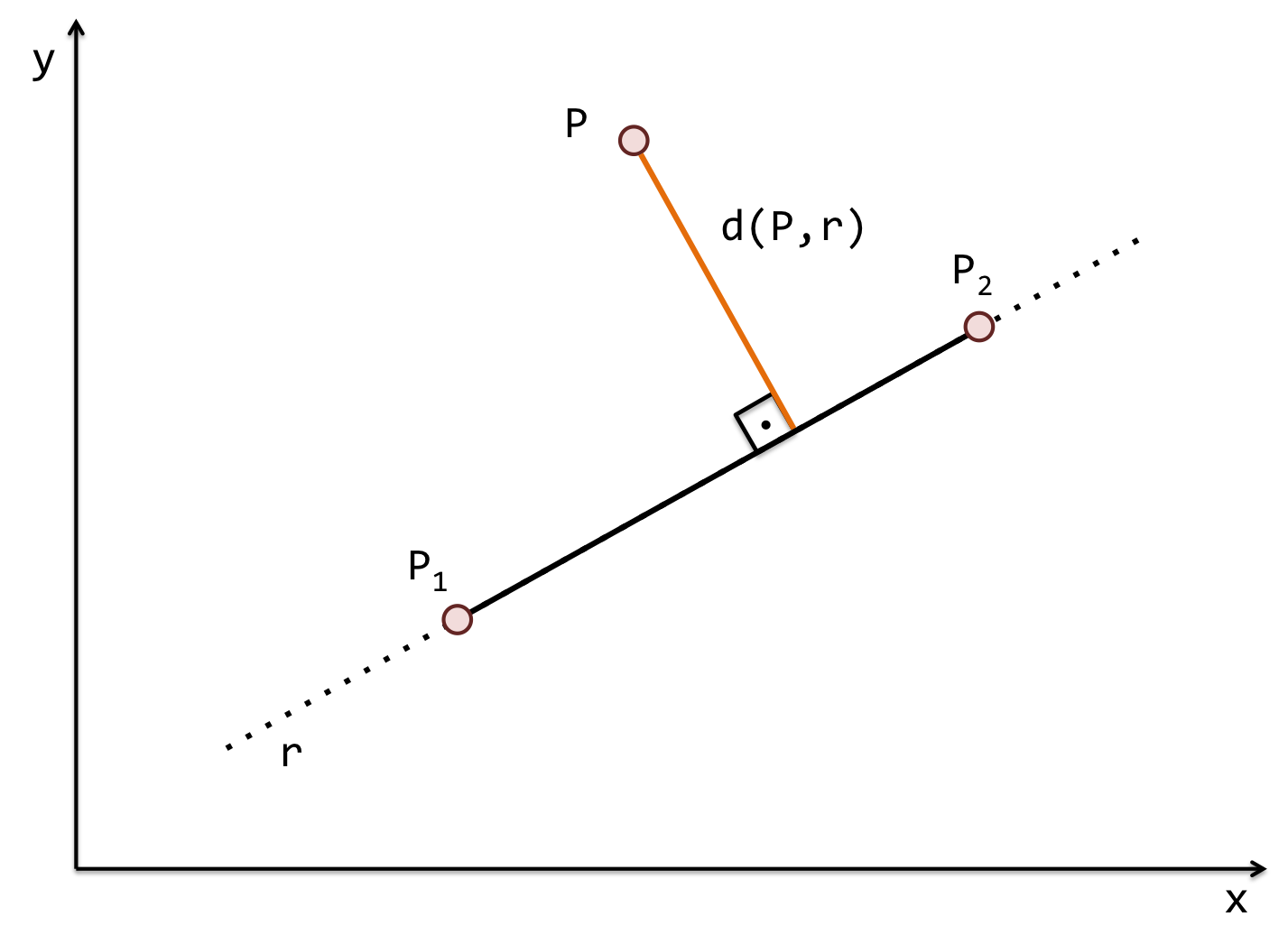
Distância mínima entre um ponto e uma reta

Figura 7.14 - Distância mínima entre um ponto e uma reta.


Uma forma de computar essa distância consiste na utilização da forma normal de Hessean para retas. Para uma reta \(r\) que passa pelos pontos \(P_1=(x_1, y_1)\) e \(P_2=(x_2, y_2)\), temos a seguinte fórmula:

(7.2)\[h(x, y) = \frac{(y_2 - y_1) \times (x - x_1) - (x_2 - x_1) \times (y - y_1)}{\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}} = 0\]

com: \(\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} > 0\).

A distância de \(P=(x, y)\) a \(r\) é dada por \(|h(x, y)|\).

Fonte: Nievergelt and Hinrichs (1993) [34].

Dica

Compare seus resultados com os da calculadora online: Distance from a point to a line - 2-Dimensional.

Aviso

O código fonte desse exercício deverá ser entregue em dois arquivos: um contendo a definição da função, com o nome ex-02-distancia-ddl.sql, e outro com um exemplo de uso da função, chamado ex-02-distancia-dml.sql.

Exercício 03. Escreva uma função que avalie se dois segmentos de reta quaisquer se interceptam ou não. Utilize como tipo do parâmetro formal dessa função dois elementos geométricos do tipo LineString (PostGIS Geometry).

Nota

Seja os segmentos de reta, \(S=\overline{P_1P_2}\) e \(T=\overline{P_3P_4}\) (Figura 7.15). Para saber se esses dois segmentos se interceptam, basta avaliar se os pontos \(P_1\) e \(P_2\) de :math`S` encontram-se em lados opostos da reta que contém o segmento \(T\), e se os pontos \(P_3\) e \(P_4\) de \(T\) estão em lados opostos da reta que contém o segmento \(S\).

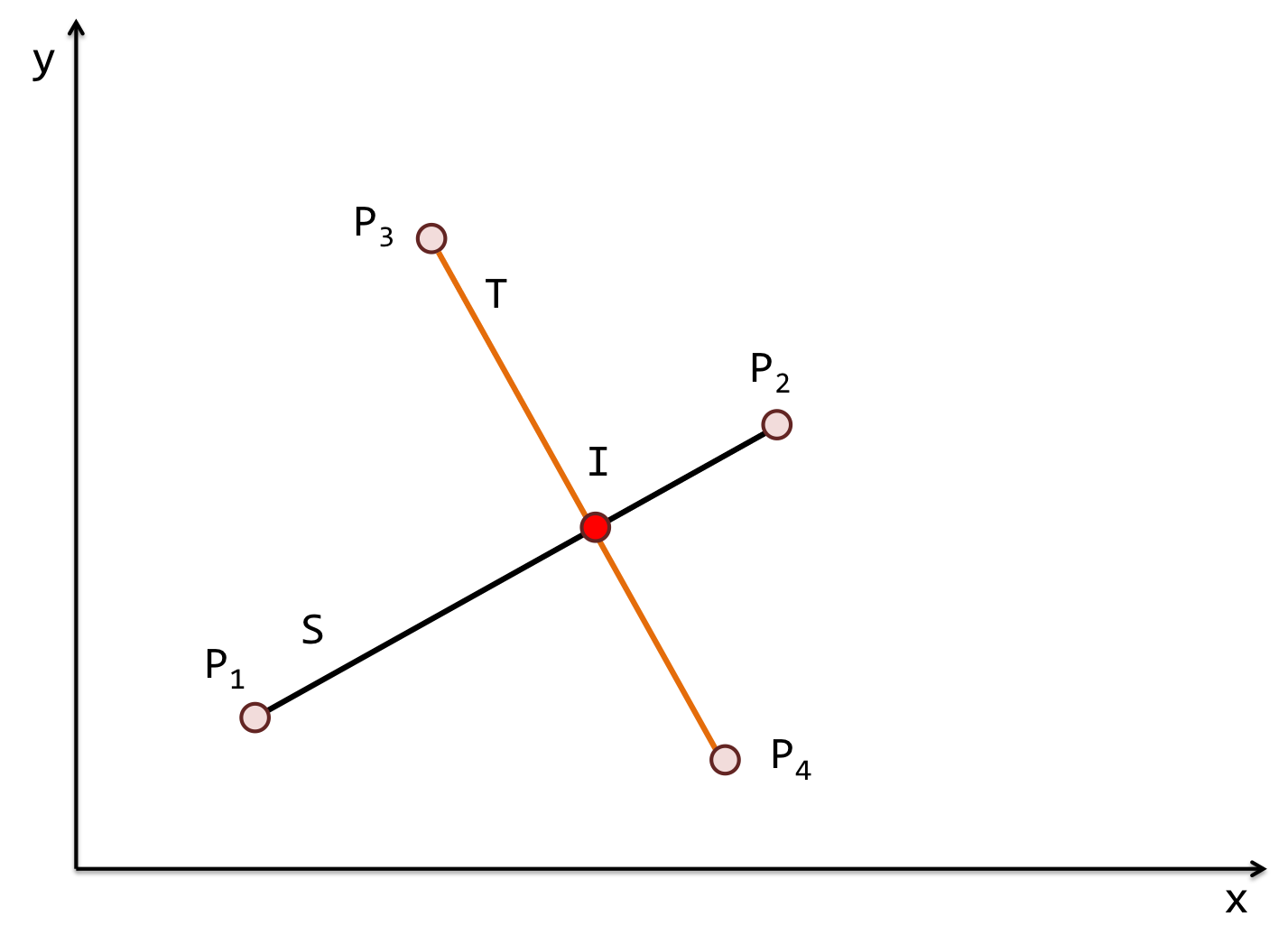
Interseção entre segmentos de reta

Figura 7.15 - Interseção entre segmentos de reta.


A equação de Hessean (Equação 7.2), mostrada no Exercício 02, pode ser usada para solução desse problema. Os pontos \(P_1\) e \(P_2\) encontram-se em lados opostos da reta que contém o segmento \(T\), se \(h(P_1) \times h(P_2) < 0\). Nesta inequação, a avaliação do denominador da equação de Hessean se torna desnecessária.

Se \(h(P_1) = 0\) ou \(h(P_2) = 0\), significa que um desses pontos encontra-se sobre a reta que contém \(T\). No caso de \(h(P_1) = 0 \land h(P_2) = 0\), os segmentos \(S\) e \(T\) são colineares e um simples teste de intervalo com os pontos extremos dos segmentos é o suficiente para dizer se há ou não interseção.

Dica

Neste exercício, a avaliação do denominador da Equação 7.2 é desnecessária.

Aviso

Veja que não é pedido no exercício para que seja computado o ponto de interseção \(I\) mostrado na Figura 7.15.

Além disso, deve ser considerado que os segmento \(S\) e \(T\) possuem interseção se eles tiverem qualquer ponto em comum, incluindo as extremidades \(P_1\), \(P_2\), \(P_3\), ou \(P_4\).

Aviso

O código fonte desse exercício deverá ser entregue em dois arquivos: um contendo a definição da função, com o nome ex-03-intersecta-ddl.sql, e outro com um exemplo de uso da função, chamado ex-03-intersecta-dml.sql.

Exercício 04. A área de um polígono simples pode ser calculada através da seguinte expressão:

\[A = \frac{1}{2} \left| \sum_{i=0}^{n-1}(x_iy_{i+1} - y_ix_{i+1}) \right|, x_n=x_0 \text{ e } y_n=y_0\]

Construa uma função que receba como parâmetro formal um polígono simples e que compute a área desse polígono.

Dica

Para mais detalhes, consulte as Seções 5.1 e 5.2.

Aviso

O código fonte desse exercício deverá ser entregue em dois arquivos: um contendo a definição da função, com o nome ex-04-area-ddl.sql, e outro com um exemplo de uso da função, chamado ex-04-area-dml.sql.

Exercício 05. Considere o diagrama apresentado na Figura 7.16:

  • Crie um arquivo denominado ex-05-modelo-ddl.sql contendo os comandos de definição das tabelas apresentadas no diagrama.

  • Crie um trigger que atualize automaticamente o periodo e a região de cobertura de uma determinada colecao quando uma nova cena é inserida na tabela cena. O arquivo contendo o código desse trigger deve se chamar ex-05-trigger-cena-colecao.sql.

  • Crie um trigger que adicione automaticamente um novo instante de tempo de uma coleção na tabela timeline quando uma nova cena for inserida na tabela cena. O arquivo contendo o código desse trigger deve se chamar ex-05-trigger-cena-timeline.sql.

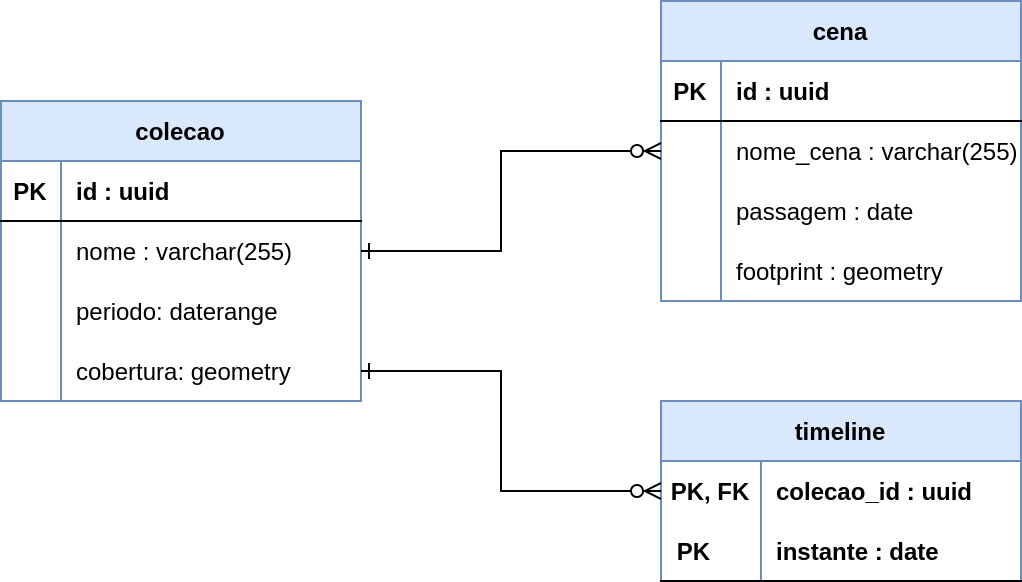
Diagrama simplificado de uma coleção de imagens

Figura 7.16 - Diagrama simplificado de uma coleção de imagens