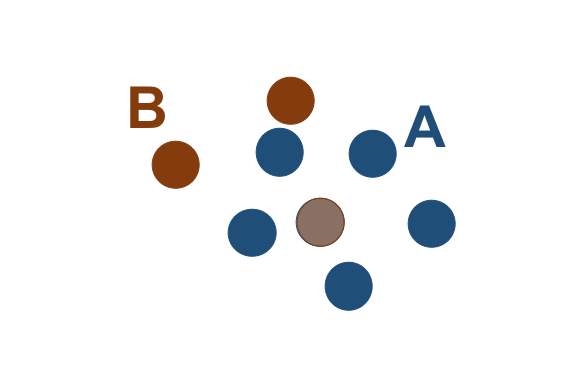3.3. Relacionamentos Espaciais

Entre as operações definidas na OGC-SFS [21], existe um conjunto que merece uma atenção especial: os operadores topológicos. Esses operadores são amplamente utilizados na construção de consultas espaciais envolvendo o relacionamento espacial entre objetos geográficos.

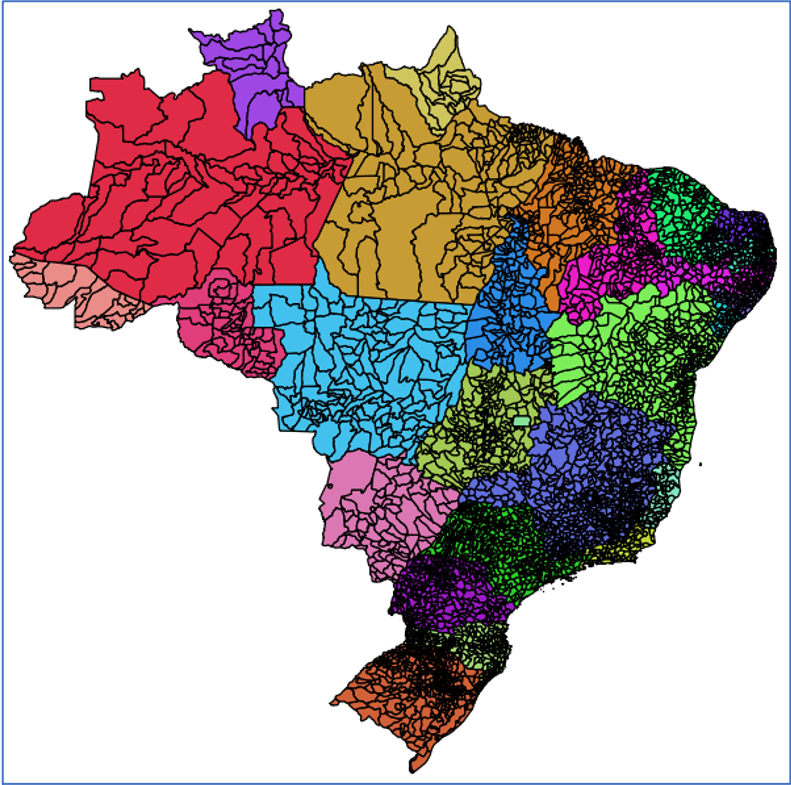
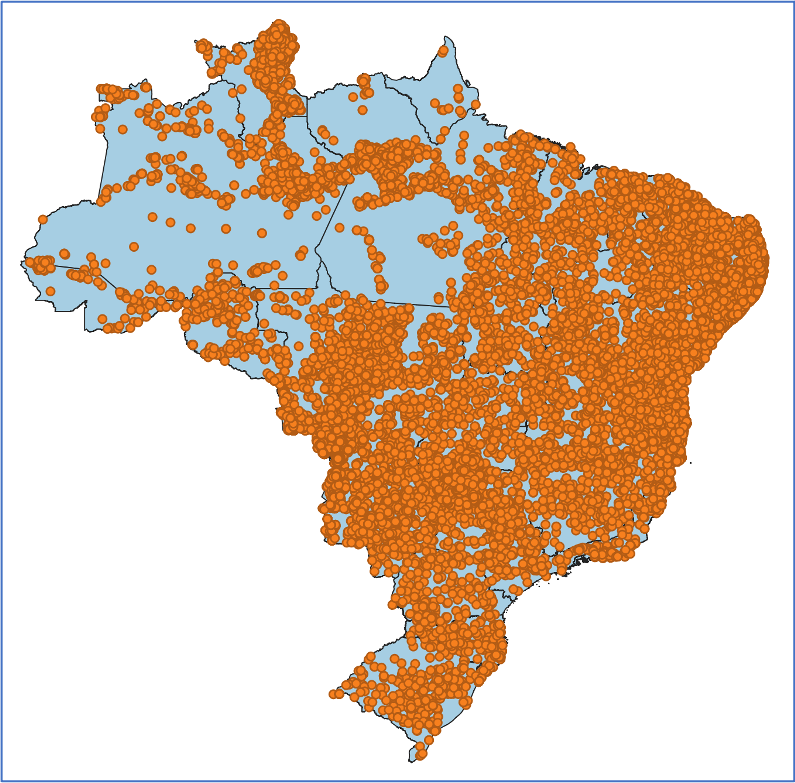
Suponha dois conjuntos de dados, um representando os limites municipais (Tabela 3.3a) e outro os focos de queimadas na vegetação (Tabela 3.3b). Para relacionar os focos de queimadas aos municípios, precisamos ser capazes de estabelecer um relacionamento espacial entre as geometrias dos municípios e as geometrias dos focos.

Tabela 3.3 - Conjuntos de Dados

( a ) Municípios Brasileiros	( b ) Focos de Queimadas na Vegetação

3.3.1. Matriz de 9-intersecções Estendida Dimensionalmente

Os relacionamentos espaciais são definidos com base no paradigma da Matriz de 9-Intersecções Estendida Dimensionalmente (DE-9IM) proposto em [10]. A abordagem básica desse método consiste em comparar dois objetos geométricos através de testes com a intersecção entre seus interiores, fronteiras e exteriores. Desta forma, podemos construir uma matrix \(3 \times 3\) como a mostrada na Tabela 3.4.

Tabela 3.4 - Matriz de 9-Intersecções Estendida Dimensionalmente.

	\(Interior(B)\)	\(Fronteira(B)\)	\(Exterior(B)\)
\(Interior(A)\)	\(dim(I(A) \cap I(B))\)	\(dim(I(A) \cap F(B))\)	\(dim(I(A) \cap E(B))\)
\(Fonteira(A)\)	\(dim(F(A) \cap I(B))\)	\(dim(F(A) \cap F(B))\)	\(dim(F(A) \cap E(B))\)
\(Exterior(A)\)	\(dim(E(A) \cap I(B))\)	\(dim(E(A) \cap F(B))\)	\(dim(E(A) \cap E(B))\)

Na matriz acima (Tabela 3.4), \(I(A)\), \(F(A)\) e \(E(A)\) referem-se, respectivamente, ao interior, fronteira e exterior do objeto \(A\). De maneira análoga, \(I(B)\), \(F(B)\) e \(E(B)\) referem-se, respectivamente, ao interior, fronteira e exterior do objeto \(B\).

A dimensionalidade máxima dos objetos resultantes da intersecção dos componentes avaliados, \(dim(x)\), pode ser:

• \(\emptyset\): Caso os componentes não tenham intersecção. Adotaremos o valor \(-1\) para este caso.

• \(0\): Se a intersecção dos componentes resulta em um ponto.

• \(1\): Se a intersecção dos componentes resulta em alguma curva.

• \(2\): Se a intersecção dos componentes resulta em alguma superfície. Adotaremos também os termos área ou região como sinônimos.

A Tabela 3.5 ilustra os conceitos de interior, fronteira e exterior para cada um dos tipos de objetos geométricos definidos na OGC-SFS.

Tabela 3.5 - Interior, fronteira e exterior dos diversos tipos geométricos.

( a ) I e E Ponto	( b ) I e E Coleção Pontos	( c ) I, F e E Curva Aberta

( d ) I e E Curva Fechada	( e ) I, F e E Col. Curv. Abertas	( f ) I e E Col. Curv. Abertas

( g ) I, F e E Polígono	( h ) I, F e E Coleção Polígonos	( i ) I, F e E Coleção Geom.

A fronteira de um objeto geométrico é formada por um conjunto de objetos geométricos de uma dimensão abaixo do objeto em questão.

Assim, a fronteira de um objeto do tipo ponto (Point) é o conjunto vazio (\(\emptyset\)), uma vez que um ponto é um objeto \(0\)-dimensional (dimensão topológica). Observe na Tabela 3.5a que no caso de um ponto, temos apenas a definição de seu interior, destacado em azul escuro, e seu exterior, representado pela região em vermelho. Portanto, o interior de um ponto é um objeto \(0\)-dimensional e seu exterior, um objeto \(2\)-dimensional.

Um objeto geométrico do tipo MultiPoint, que também é \(0\)-dimensional, tem sua fronteira definida como o conjunto vazio (\(\emptyset\)). O interior é formado pelos próprios pontos da coleção, destacados em azul escuro na Tabela 3.5b, e o exterior é região destacada em vermelho nessa tabela.

A fronteira de uma curva aberta (Curve) consiste nos pontos inicial e final dessa curva. A Tabela 3.5c mostra uma exemplo de curva aberta, onde os pontos destacados em verde formam a fronteira dessa curva. Portanto, a fronteira de uma curva aberta é um conjunto de objetos geométricos \(0\)-dimensional. O interior de uma curva aberta é formado pelos infinitos pontos de sua imagem, exceto os pontos da fronteira. Na Tabela 3.5c, a linha em azul escuro corresponde ao interior da curva, que é um objeto geométrico \(1\)-dimensional. O exterior da curva é representado pela região em vermelho que não contém os pontos da fronteira e do interior da curva.

A fronteira de uma curva fechada (Curve) é o conjunto vazio (\(\emptyset\)). A Tabela 3.5d mostra um exemplo de curva fechada. Nessa tabela, podemos observar que o interior é formado por todos os pontos da curva, incluindo os pontos inicial e final, formando um objeto geométrico \(1\)-dimensional. O exterior de uma curva fechada é uma região, um objeto \(2\)-dimensional, destacado em vermelho nessa tabela.

A fronteira de uma coleção de curvas (MultiCurve) consiste nos pontos na fronteira de um número ímpar de elementos da curva. A Tabela 3.5e mostra um exemplo de coleção de curvas abertas. Repare que os pontos destacados em verde formam a fronteira dessa curva, enquanto os pontos sobre as imagens das linhas, destacados em azul escuro, forma seus interiores e seu exterior é destacado pela região em vermelho. A Tabela 3.5f ilustra a regra de que os pontos da fronteira devem pertencer a um número ímpar de elementos da curva.

Uma coleção de curvas (MultiCurve) é dita fechada se todos os seus elementos são fechados, consequentemente, a fronteira de uma coleção de curvas fechadas é o conjunto vazio (\(\emptyset\)).

A fronteira de um polígono (Polygon) consiste no seu conjunto de anéis (LinearRing). A Tabela 3.5g ilustra esse caso. Repare que o exterior de um polígono com buraco é desconectado.

A fronteira de uma coleção de polígonos (MultiPolygon) consiste no conjunto de anéis (LinearRing) de seus polígonos (Polygon) (Tabela 3.5h).

A fronteira de um conjunto de objetos geométricos heterogêneos (GeometryCollection) cujo os interiores dos seus elementos são disjuntos, consiste nos objetos geométricos das fronteiras desses elementos obedecendo à regra de que os pontos devem pertencer a um número ímpar de elementos (Tabela 3.5i).

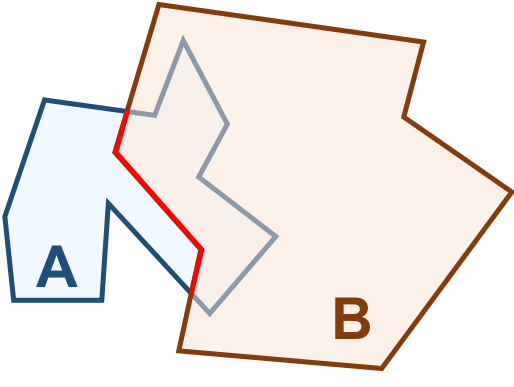
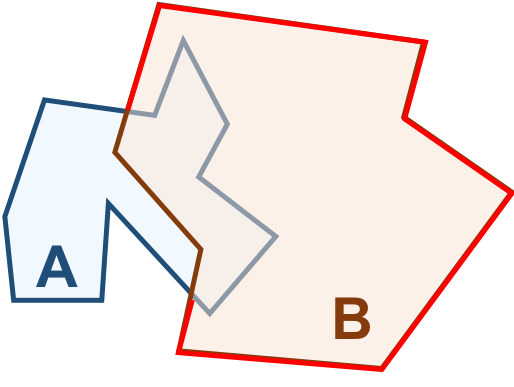
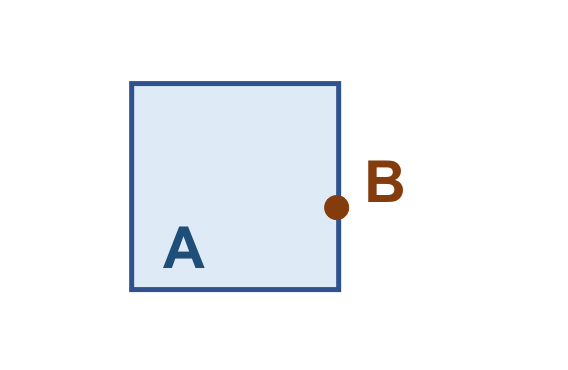
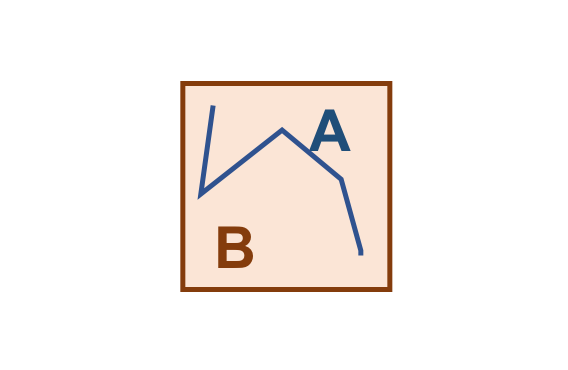
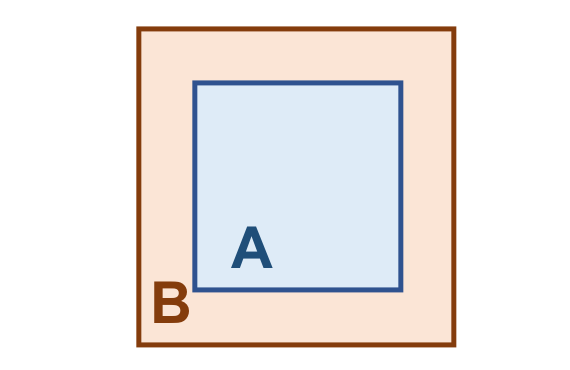
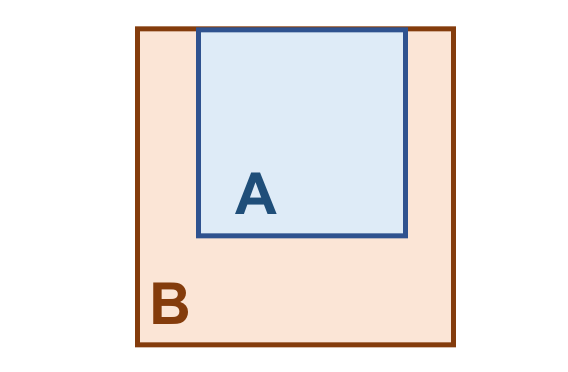
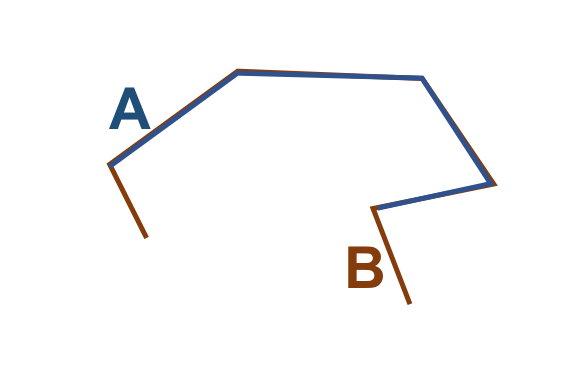
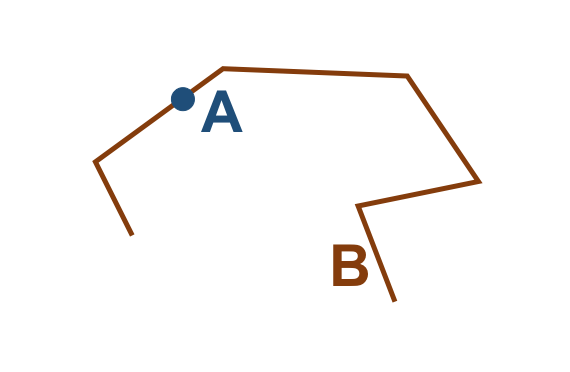
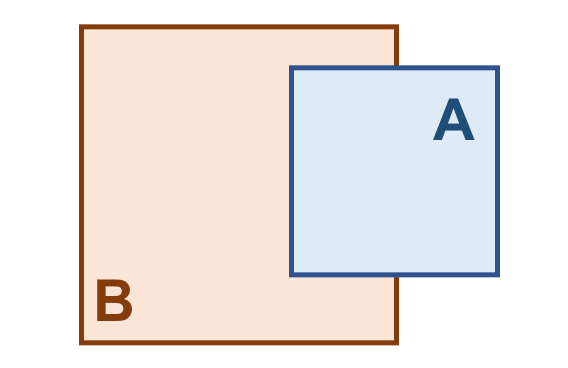
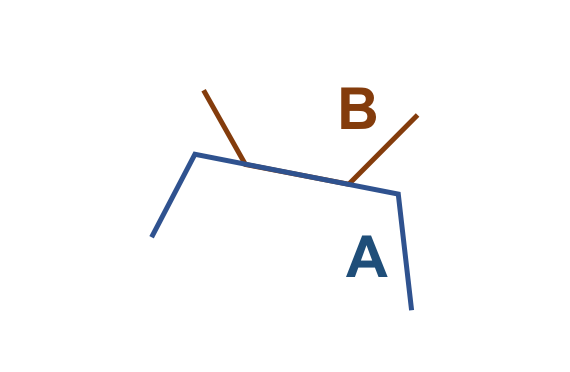
Vamos considerar os objetos geométricos apresentados na Figura 3.4. Podemos estabelecer o seguinte:

• \(I(A)\): área mostrada em azul claro.

• \(F(A)\): formada por um único anel (externo), em azul escuro.

• \(E(A)\): é definido como toda a região do espaço que não compreenda a fronteira e o interior de \(A\).

De maneira análoga:

• \(I(B)\): área mostrada em laranja claro.

• \(F(B)\): formada por um único anel (externo), em laranja escuro.

• \(E(B)\): é definido como toda a região do espaço que não compreenda a fronteira e o interior de \(B\).

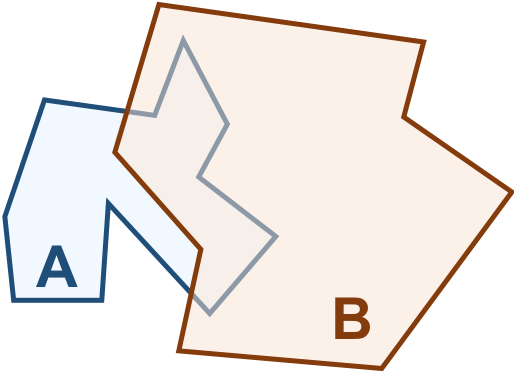
Figura 3.4 - Configuração espacial de dois objetos geométricos \(A\) e \(B\).

O relacionamento espacial definido por \(A\) e \(B\), segundo a matriz de intersecções, é o seguinte:

Tabela 3.6 - DE-9IM - \(A\) e \(B\).

	\(Interior(B)\)	\(Fronteira(B)\)	\(Exterior(B)\)
\(Interior(A)\)	\(2\)	\(1\)	\(2\)
\(Fonteira(A)\)	\(1\)	\(0\)	\(1\)
\(Exterior(A)\)	\(2\)	\(1\)	\(2\)

A matriz acima foi definida considerando:

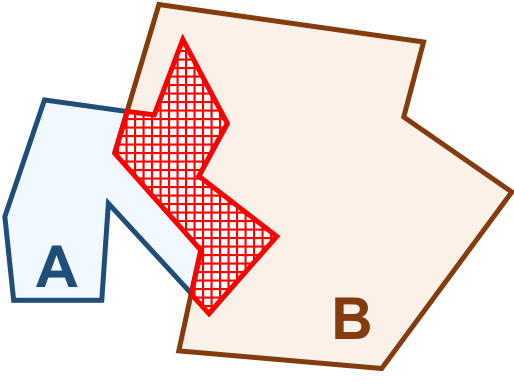
• Os interiores de \(A\) e \(B\) são regiões, isto é, objetos \(2\)-dimensional. A intersecção desses dois componentes forma uma nova região, a área em vermelho na Tabela 3.7a, que também é um objeto \(2\)-dimensional. Logo, a \(dim(I(A) \cap I(B)) = 2\).

• A fronteira de \(B\) é formada por um anel (laranja), um objeto \(1\)-dimensional. A intersecção entre \(I(A)\) e a \(F(B)\) forma uma linha, destacada em vermelho na Tabela 3.7b, que é um objeto \(1\)-dimensional. Logo, a \(dim(I(A) \cap F(B)) = 1\).

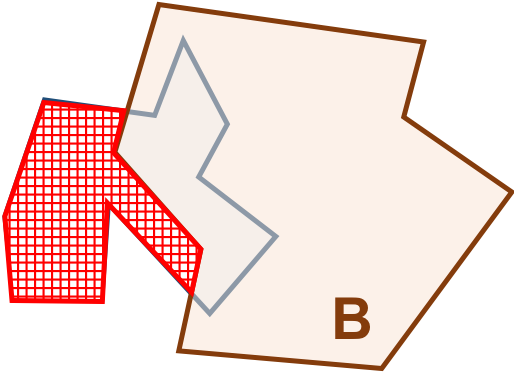
• O exterior de \(B\) é uma região. A intersecção do \(I(A)\) e o \(E(B)\) forma a área destacada em vermelho da Tabela 3.7c. Logo, a \(dim(I(A) \cap E(B)) = 2\).

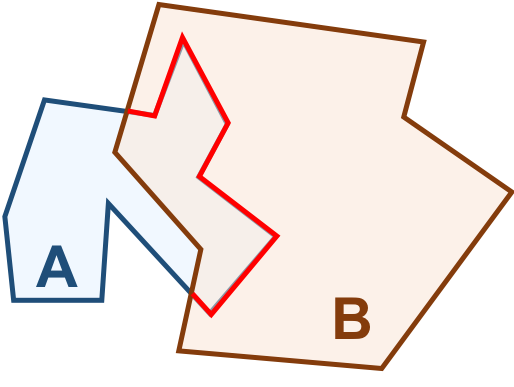
• A fronteira de \(A\) é formada por um anel (azul). A intersecção entre \(F(A)\) e o \(I(B)\) forma uma linha, destacada em vermelho na Tabela 3.7d, que é um objeto \(1\)-dimensional. Logo, a \(dim(F(A) \cap I(B)) = 1\).

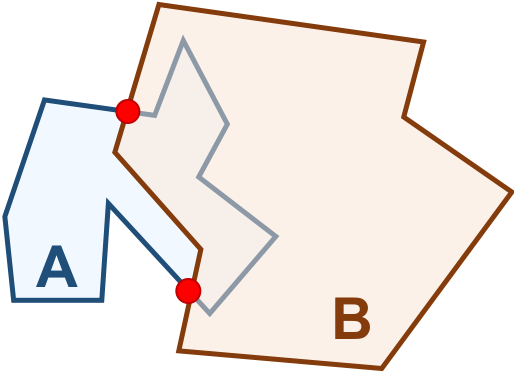
• A intersecção entre as fronteiras de \(A\) e \(B\) são os pontos mostrados em vermelho na Tabela 3.7e. Como um ponto é um objeto \(0\)-dimensional, a \(dim(F(A) \cap F(B)) = 0\).

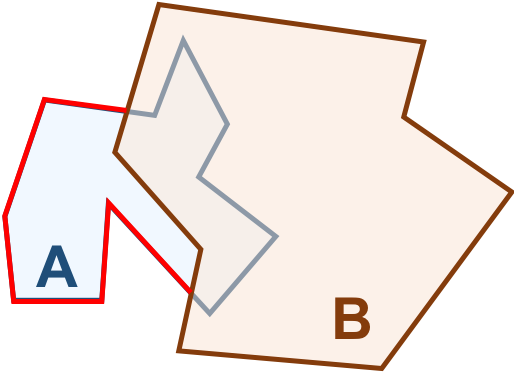
• A intersecção entre a fronteira de \(A\) e o exterior de \(B\) forma a linha mostrada na Tabela 3.7f. Logo, a \(dim(F(A) \cap E(B)) = 1\).

• A intersecção entre exterior de \(A\) e interior de \(B\) forma uma área (Tabela 3.7g). Logo, a \(dim(E(A) \cap I(B)) = 2\).

• A intersecção entre exterior de \(A\) e fronteira de \(B\) forma a linha mostrada na Tabela 3.7h. Logo, a \(dim(E(A) \cap F(B)) = 1\).

• A interseção entre os exteriores de \(A\) e \(B\) formam uma área (Tabela 3.7i). Logo, a \(dim(E(A) \cap E(B)) = 2\).

Tabela 3.7 - Intersecção entre os componentes dos objetos \(A\) e \(B\).

( a ) \(I(A) \cap I(B)\)	( b ) \(I(A) \cap F(B)\)	( c ) \(I(A) \cap E(B)\)

( d ) \(F(A) \cap I(B)\)	( e ) \(F(A) \cap F(B)\)	( f ) \(F(A) \cap E(B)\)

( d ) \(E(A) \cap I(B)\)	( e ) \(E(A) \cap F(B)\)	( f ) \(E(A) \cap E(B)\)

3.3.2. Operador Relate

Em geral, os ambientes computacionais que dão suporte a OGC-SFS, introduzem uma função chamada Relate que permite determinar a matriz de intersecções ou testar se dois objetos satisfazem um determinado padrão dessa matriz. Assim, tanto em Python quanto em C++, ou Java, ou em SQL, é possível testar o relacionamento espacial entre dois objetos usando um operador chamado Relate (ou uma variação desse nome).

O exemplo abaixo mostra como seria o uso dessa função para saber o relacionamento espacial entre dois polígonos hipotéticos:

A = Polygon(...)
B = Polygon(...)

M = Relate(A, B)

Nesse caso, M é a matriz resultante do relacionamento espacial entre A e B. Se A e B forem os polígonos mostrados na Figura 3.4, teríamos M codificado como a seguinte string: "212101212".

O próximo exemplo mostra como seria a utlização da função Relate para saber se dois objetos A e B satisfazem um padrão específico da matriz de intersecções:

A = Polygon(...)
B = Polygon(...)

M = "212101212"

resultado = Relate(A, B, M)

print(resultado)

Nesse caso, M é a matriz com o padrão que desejamos verificar se os objetos A e B satisfazem. Se A e B forem os polígonos mostrados na Figura 3.4, essa função retorna o valor booleano True.

3.3.3. Relacionamentos Espaciais Nomeados

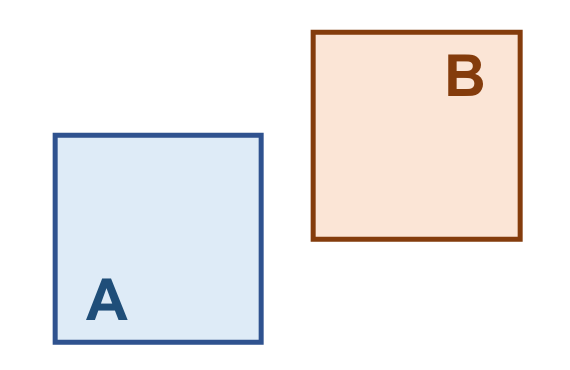
Para facilitar a construção de predicados topológicos nas consultas espaciais existe um conjunto de oito operadores com nomes bem definidos que são baseados na sobrecarga de alguns padrões da matriz de intersecções. Os operadores nomeados são: Equals, Touches, Crosses, Within, Contains, Overlaps, Disjoint, and Intersects. Esses operadores comparam pares de geometrias e são definidos utilizando os seguintes valores para as células da matriz de intersecções:

• T: indica que \(dim(x) \in \{0, 1, 2\}\), ou seja, \(x \neq \emptyset\). Em outras palavras, o resultado da intersecção é um objeto \(x\) que pode ser qualquer elemento geométrico (ponto, curva ou superfície).

• F: indica que \(dim(x) = \emptyset\), ou seja, \(x = \emptyset\). Em outras palavras, o resultado da intersecção é um conjunto vazio. Adotaremos que \(dim(x) = \emptyset \implies dim(x) = -1\), de maneira que usaremos \(-1\) quando necessário para indicar que a intersecção é vazia.

• *: indica que \(dim(x) \in \{-1, 0, 1, 2\}\), ou seja, não importa se há ou não intersecção.

• 0: indica que \(dim(x) = 0\), ou seja, que a dimensão máxima do elemento geométrico resultante da intersecção é zero, isto é, um ponto.

• 1: indica que \(dim(x) = 1\), ou seja, que a dimensão máxima do elemento geométrico resultante da intersecção é uma curva.

• 2: indica que \(dim(x) = 2\), ou seja, que a dimensão máxima do elemento geométrico resultante da intersecção é uma superfície (ou área).

Além disso, em alguns casos diferenciamos os padrões pelos tipos de objetos testados. Usamos a seguinte nomenclatura para os tipos de objetos:

• Pontuais ou P: pontos e coleções homogêneas de pontos.

• Curvas ou L: linhas, anéis, ou coleções homogêneas de linhas.

• Superfícies ou A: polígonos ou coleções homogêneas de polígonos.

3.3.3.1. \(Equals(Geometry, Geometry) \rightarrow bool\)

Retorna verdadeiro (True) se as duas geometrias são espacialmente iguais. Neste caso, a matriz de intersecção para as duas geometrias deve satisfazer o seguinte padrão:

Tabela 3.8 - DE-9IM - \(Equals(Geometry, Geometry) \rightarrow bool\).

	\(Interior(B)\)	\(Fronteira(B)\)	\(Exterior(B)\)
\(Interior(A)\)	\(T\)	\(F\)	\(F\)
\(Fonteira(A)\)	\(F\)	\(T\)	\(F\)
\(Exterior(A)\)	\(F\)	\(F\)	\(T\)

Pela matriz acima, o relacionamento Equals garante que os interiores das duas geometrias tenham intersecção e que os interiores e fronteiras de um objeto não tenham intersecção com o exterior do outro.

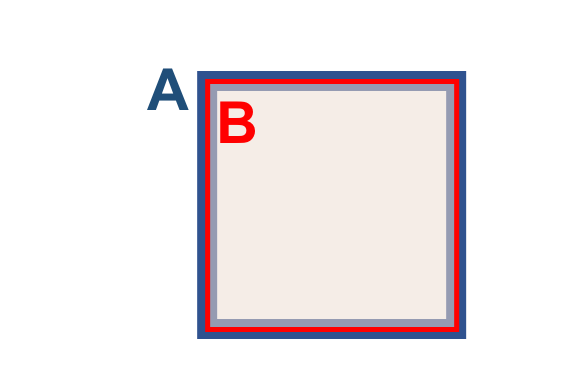
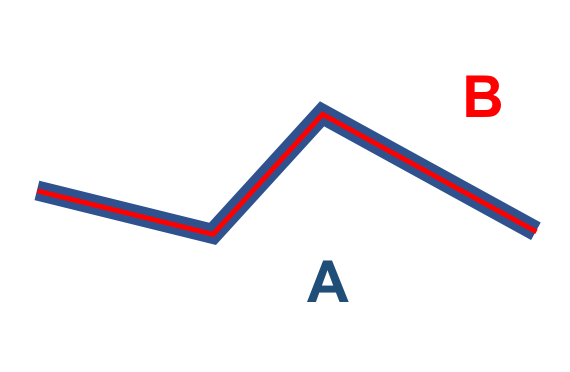
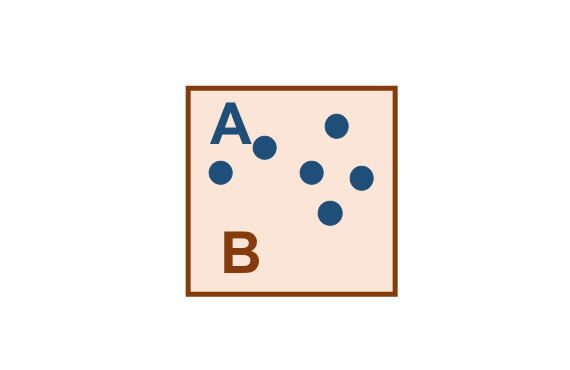
A Tabela 3.9 apresenta alguns pares de objetos que satisfazem o relacionamento espacial Equals, de acordo com o padrão mostrado acima:

Tabela 3.9 - \(A\) e \(B\) são geometrias espacialmente iguais.

( a )	( b )	( c )

Nota

No caso dos pares de geometrias serem curvas/curvas ou superfícies/superfícies, mesmo que o número de pontos desses objetos sejam diferentes, o relacionamento Equals pode ser verdadeiro.

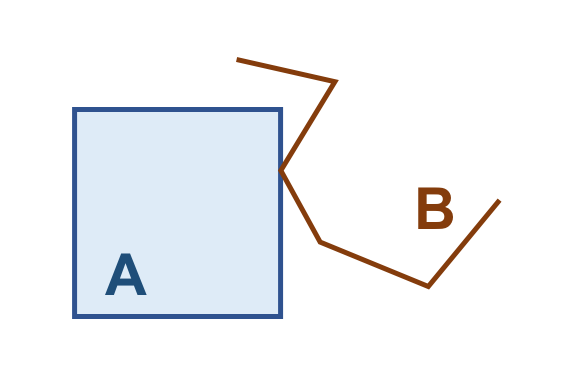
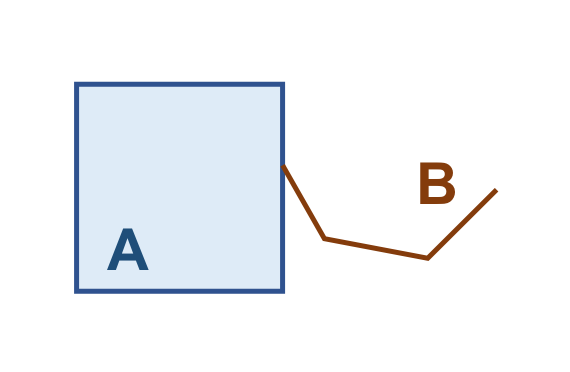
3.3.3.2. \(Touches(Geometry, Geometry) \rightarrow Bool\)

Retorna verdadeiro (True) se as duas geometrias se tocam. Este relacionamento espacial é definido para os casos onde os pares de objetos geométricos correspondem a A/A, L/L, L/A, P/A e P/L. Este relacionamento não se aplica no caso dos objetos serem do tipo P/P.

Se os pares de objetos satisfizerem um dos três padrões mostrados abaixo, dizemos que a geometria \(A\) toca a geometria \(B\):

Tabela 3.10 - DE-9IM - \(Touches(Geometry, Geometry) \rightarrow bool\).

	\(Interior(B)\)	\(Fronteira(B)\)	\(Exterior(B)\)
\(Interior(A)\)	\(F\)	\(T\)	\(*\)
\(Fonteira(A)\)	\(*\)	\(*\)	\(*\)
\(Exterior(A)\)	\(*\)	\(*\)	\(*\)

Tabela 3.11 - DE-9IM - \(Touches(Geometry, Geometry) \rightarrow bool\).

	\(Interior(B)\)	\(Fronteira(B)\)	\(Exterior(B)\)
\(Interior(A)\)	\(F\)	\(*\)	\(*\)
\(Fonteira(A)\)	\(T\)	\(*\)	\(*\)
\(Exterior(A)\)	\(*\)	\(*\)	\(*\)

Tabela 3.12 - DE-9IM - \(Touches(Geometry, Geometry) \rightarrow bool\).

	\(Interior(B)\)	\(Fronteira(B)\)	\(Exterior(B)\)
\(Interior(A)\)	\(F\)	\(*\)	\(*\)
\(Fonteira(A)\)	\(*\)	\(T\)	\(*\)
\(Exterior(A)\)	\(*\)	\(*\)	\(*\)

Os três padrões acima estabelecem que os objetos não podem ter intersecção entre seus interiores, mas podem ter intersecção entre as fronteiras ou entre a fronteira de um e o interior do outro.

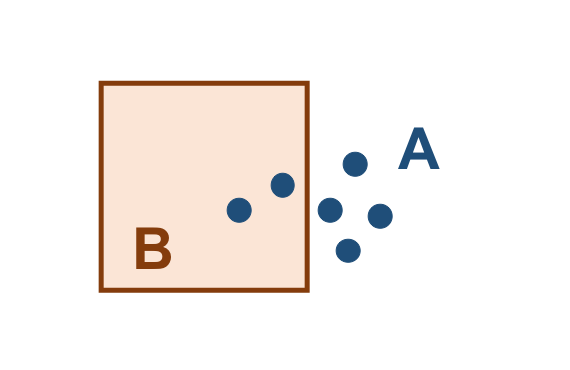
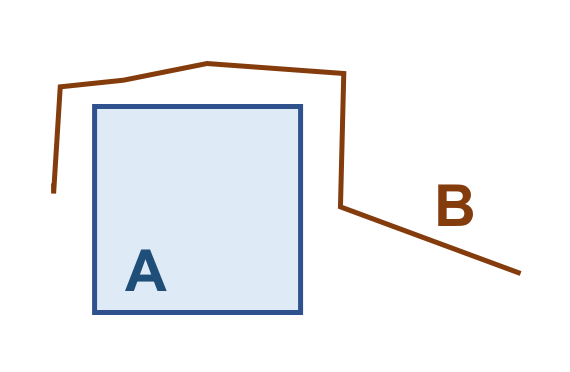
A Tabela 3.13 apresenta alguns pares de objetos que satisfazem o relacionamento espacial Touches, de acordo com os padrões mostrados acima:

Tabela 3.13 - \(A\) e \(B\) são geometrias que se tocam.

( a )	( b )	( c )	( d )

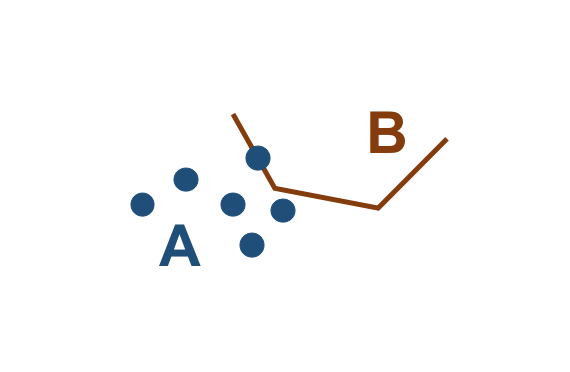
3.3.3.3. \(Crosses(Geometry, Geometry) \rightarrow bool\)

Retorna verdadeiro (True) se a primeira geometria cruza a segunda. Este relacionamento espacial é definido para os casos P/L, P/A, L/L e L/A.

O resultado da intersecção entre duas geometrias deve gerar uma outra de dimensão um nível menor do que a maior dimensão das geometrias envolvidas e os interiores devem ter intersecção.

Nos casos P/L, P/A, ou L/A:

Tabela 3.14 - DE-9IM - \(Crosses(Geometry, Geometry) \rightarrow bool\).

	\(Interior(B)\)	\(Fronteira(B)\)	\(Exterior(B)\)
\(Interior(A)\)	\(T\)	\(*\)	\(T\)
\(Fonteira(A)\)	\(*\)	\(*\)	\(*\)
\(Exterior(A)\)	\(*\)	\(*\)	\(*\)

No caso L/L:

Tabela 3.15 - DE-9IM - \(Crosses(Geometry, Geometry) \rightarrow bool\).

	\(Interior(B)\)	\(Fronteira(B)\)	\(Exterior(B)\)
\(Interior(A)\)	\(0\)	\(*\)	\(*\)
\(Fonteira(A)\)	\(*\)	\(*\)	\(*\)
\(Exterior(A)\)	\(*\)	\(*\)	\(*\)

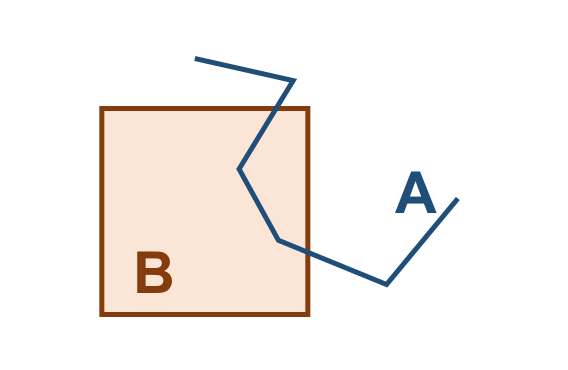
A Tabela 3.16 apresenta alguns pares de objetos que satisfazem o relacionamento espacial Crosses, de acordo com os padrões mostrados acima:

Tabela 3.16 - \(A\) e \(B\) são geometrias que se cruzam.

( a )	( b )	( c )	( d )

3.3.3.4. \(Within(Geometry, Geometry) \rightarrow bool\)

Retorna verdadeiro (True) se a primeira geometria está dentro da segunda e se elas não são iguais.

O padrão da matriz para este relacionamento espacial é o seguinte:

Tabela 3.17 - DE-9IM - \(Within(Geometry, Geometry) \rightarrow bool\).

	\(Interior(B)\)	\(Fronteira(B)\)	\(Exterior(B)\)
\(Interior(A)\)	\(T\)	\(*\)	\(F\)
\(Fonteira(A)\)	\(*\)	\(*\)	\(F\)
\(Exterior(A)\)	\(*\)	\(*\)	\(*\)

A matriz acima define que o predicado Within retorna True quando os interiores das duas geometrias possuem intersecção e quando o interior e a fronteira do objeto A não têm intersecção com o exterior de B. O uso do padrão * nas demais células indica que nenhuma outra condição importa para determinar este relacionamento.

A Tabela 3.18 apresenta alguns pares de objetos que satisfazem o relacionamento espacial Within, de acordo com os padrões mostrados acima:

Tabela 3.18 - A geometria \(A\) está dentro da geometria \(B\).

( a )	( b )	( c )

( d )	( e )	( f )

3.3.3.5. \(Contains(GeometryA, GeometryB) \rightarrow bool\)

Retorna verdadeiro (True) se a primeira geometria contém a segunda e se elas não são iguais. Este relacionamento espacial é o inverso de Within, de maneira que temos:

\(Contains(A, B) \iff Within(B, A)\)

A matriz de intersecções do predicado Contains é a seguinte:

Tabela 3.19 - DE-9IM - \(Contains(Geometry, Geometry) \rightarrow bool\).

	\(Interior(B)\)	\(Fronteira(B)\)	\(Exterior(B)\)
\(Interior(A)\)	\(T\)	\(*\)	\(*\)
\(Fonteira(A)\)	\(*\)	\(*\)	\(*\)
\(Exterior(A)\)	\(F\)	\(F\)	\(*\)

Na matriz acima podemos observar que os interiores das duas geometrias devem ter intersecção e que a fronteira e interior da segunda (B) não pode ter intersecção com o exterior da primeira (A).

3.3.3.6. \(Overlaps(Geometry, Geometry) \rightarrow bool\)

Retorna verdadeiro (True) se a primeira geometria sobrepõe a segunda. Este relacionamento espacial é definido para os casos A/A, L/L e P/P. Em outras palavras, este relacionamento só é válido para geometrias de mesma dimensão e se a intersecção entre elas resultar em um objeto de mesma dimensão.

No caso P/P ou A/A, o predicado Overlap retorna True se os interiores das duas geometria possuem intersecção e se o interior de uma faz intersecção com o exterior da outra e vice-versa. Este relacionamento é definido através do seguinte padrão:

Tabela 3.20 - DE-9IM - \(Overlaps(Geometry, Geometry) \rightarrow bool\).

	\(Interior(B)\)	\(Fronteira(B)\)	\(Exterior(B)\)
\(Interior(A)\)	\(T\)	\(*\)	\(T\)
\(Fonteira(A)\)	\(*\)	\(*\)	\(*\)
\(Exterior(A)\)	\(T\)	\(*\)	\(*\)

No caso L/L, a intersecção deve resultar em um objeto \(1\)-dimensional. Assim, temos o seguinte padrão de matriz:

Tabela 3.21 - DE-9IM - \(Overlaps(Geometry, Geometry) \rightarrow bool\).

	\(Interior(B)\)	\(Fronteira(B)\)	\(Exterior(B)\)
\(Interior(A)\)	\(1\)	\(*\)	\(T\)
\(Fonteira(A)\)	\(*\)	\(*\)	\(*\)
\(Exterior(A)\)	\(T\)	\(*\)	\(*\)

A Tabela 3.18 apresenta alguns pares de objetos que satisfazem o relacionamento espacial Overlaps, de acordo com os padrões mostrados acima:

Tabela 3.22 - A geometria \(A\) sobrepõe a geometria \(B\).

( a )	( b )	( c )

3.3.3.7. \(Disjoint(Geometry, Geometry) \rightarrow bool\)

Retorna verdadeiro (True) se as duas geometrias não possuem qualquer tipo de interação espacial, isto é, se os interiores e fronteiras não possuem qualquer intersecção, exceto com os exteriores. Neste caso, a matriz de intersecção para as duas geometrias deve satisfazer o seguinte padrão:

Tabela 3.23 - DE-9IM - \(Disjoint(Geometry, Geometry) \rightarrow bool\).

	\(Interior(B)\)	\(Fronteira(B)\)	\(Exterior(B)\)
\(Interior(A)\)	\(F\)	\(F\)	\(*\)
\(Fonteira(A)\)	\(F\)	\(F\)	\(*\)
\(Exterior(A)\)	\(*\)	\(*\)	\(*\)

A matriz acima define que no relacionamento Disjoint nem a fronteira, nem o interior de um objeto possui intersecção com a fronteira ou interior do outro objeto.

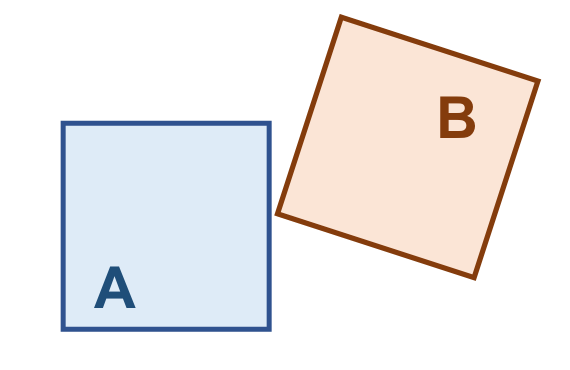
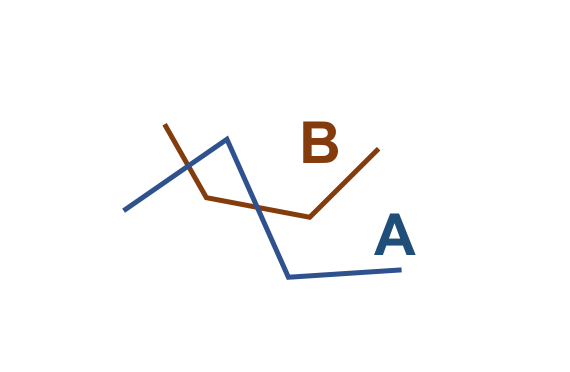
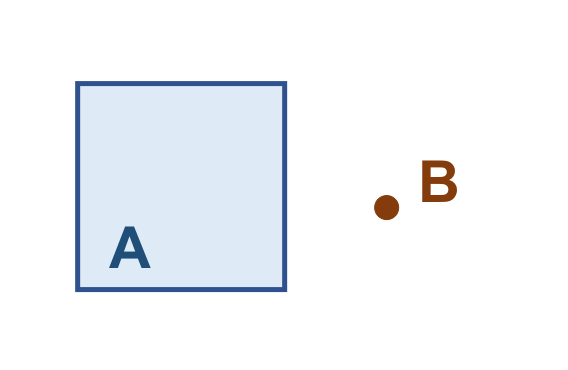
A Tabela 3.24 apresenta alguns pares de objetos que satisfazem o relacionamento espacial Disjoint, de acordo com o padrão mostrado acima:

Tabela 3.24 - \(A\) e \(B\) são geometrias espacialmente disjuntas.

( a )	( b )	( c )

3.3.3.8. \(Intersects(Geometry, Geometry) \rightarrow bool\)

Retorna verdadeiro (True) se as duas geometrias tiverem algum tipo de interação espacial, isto é, se os interiores e fronteiras tiverem qualquer intersecção. Este relacionamento espacial é definido como sendo a negação do relacionamento Disjoint:

\(Intersects(A, B) \iff \neg Disjoint(A, B)\)

Na verdade esse relacionamento diz que as geometrias \(A\) e \(B\) podem se tocar, ou cruzar, ou sobrepor, ou uma estar contida uma na outra, ou serem iguais. Define-se este relacionamento para facilitar a escrita de expressões com predicados espaciais.

Portanto, o predicado Intersects retorna True se os interiores das duas geometrias se intersectam:

Tabela 3.25 - DE-9IM - \(Intersects(Geometry, Geometry) \rightarrow bool\).

	\(Interior(B)\)	\(Fronteira(B)\)	\(Exterior(B)\)
\(Interior(A)\)	\(T\)	\(*\)	\(*\)
\(Fonteira(A)\)	\(*\)	\(*\)	\(*\)
\(Exterior(A)\)	\(*\)	\(*\)	\(*\)

Se as fronteiras das duas geometrias se intersectam:

Tabela 3.26 - DE-9IM - \(Intersects(Geometry, Geometry) \rightarrow bool\).

	\(Interior(B)\)	\(Fronteira(B)\)	\(Exterior(B)\)
\(Interior(A)\)	\(*\)	\(*\)	\(*\)
\(Fonteira(A)\)	\(*\)	\(T\)	\(*\)
\(Exterior(A)\)	\(*\)	\(*\)	\(*\)

Se o interior da primeira intersecta a fronteira da segunda:

Tabela 3.27 - DE-9IM - \(Intersects(Geometry, Geometry) \rightarrow bool\).

	\(Interior(B)\)	\(Fronteira(B)\)	\(Exterior(B)\)
\(Interior(A)\)	\(*\)	\(T\)	\(*\)
\(Fonteira(A)\)	\(*\)	\(*\)	\(*\)
\(Exterior(A)\)	\(*\)	\(*\)	\(*\)

Ou se a fronteira da primeira intersecta o interior da segunda:

Tabela 3.28 - DE-9IM - \(Intersects(Geometry, Geometry) \rightarrow bool\).

	\(Interior(B)\)	\(Fronteira(B)\)	\(Exterior(B)\)
\(Interior(A)\)	\(*\)	\(*\)	\(*\)
\(Fonteira(A)\)	\(T\)	\(*\)	\(*\)
\(Exterior(A)\)	\(*\)	\(*\)	\(*\)