4.1. Aproximações Geométricas

O retângulo envolvente mínimo (REM) é uma das aproximações mais utilizadas em aplicações geoespaciais para geometrias do tipo polígonais e lineares. A Figura 4.1 apresenta o retângulo envolvente da geometria representando os limites territoriais do Brasil (um MultiPolygon). O que faz o REM ser uma aproximação muito utilizada é o fato de que, no espaço bidimensional, apenas um par de pontos seja necessário para representá-lo \((X_{min}, X_{max}, Y_{min}, Y_{max})\).

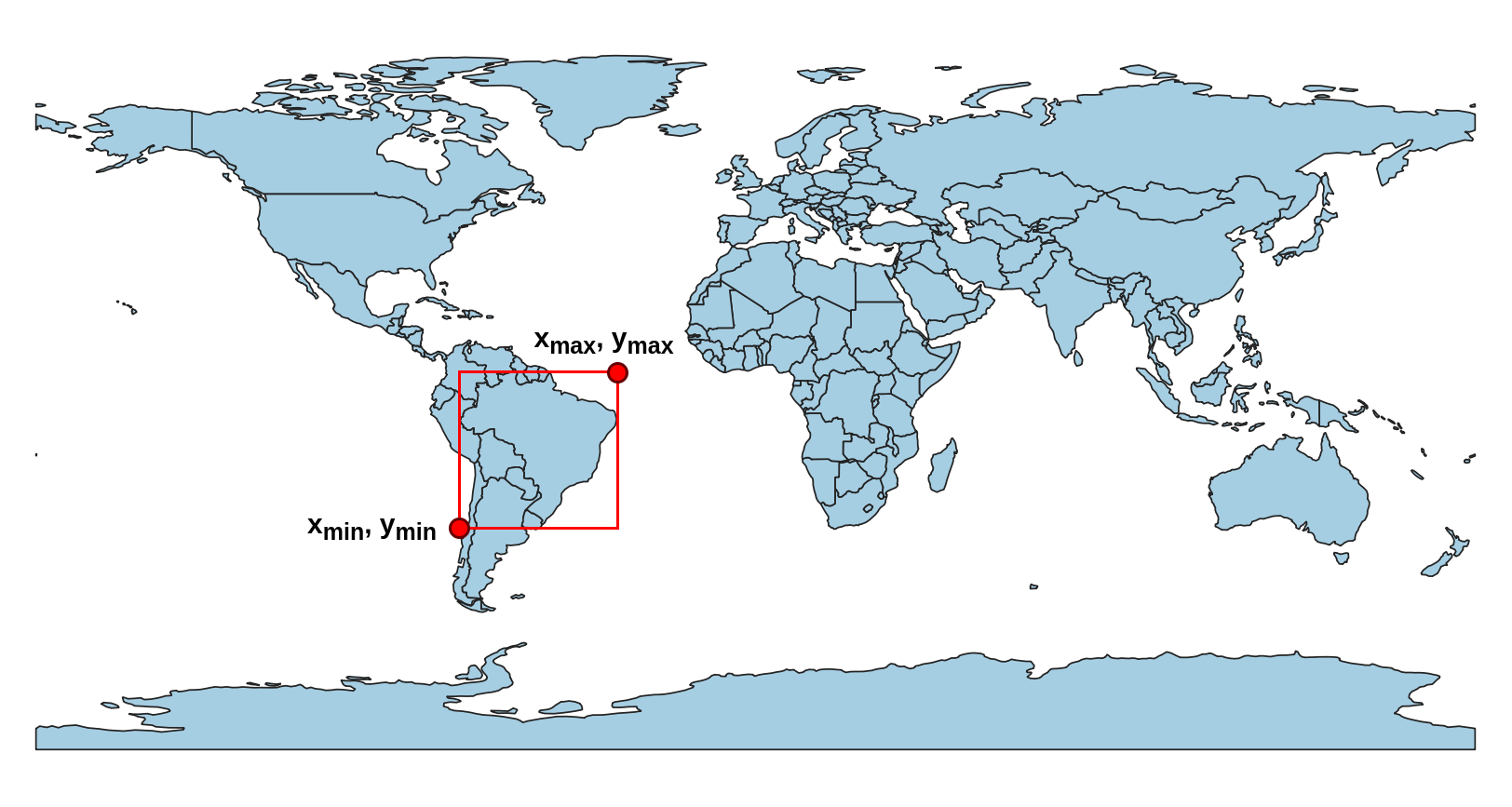
Figura 4.1 - Retângulo envolvente da geometria representando os limites territoriais do Brasil.

Nota

O REM muitas vezes é chamado de Minimum Bounding Box (MBB) ou Bounding Box (BBOX).

Além disso, o REM funciona como um filtro rápido para testes de relacionamento espacial. Considere a Figura 4.2, quando os REM de duas geometrias não possuem intersecção, então essas duas geometrias com certeza serão disjuntas. Portanto, um simples teste com o REM das geometrias é suficiente para descartar o processamento considerando todos os vértices dessas geometrias.

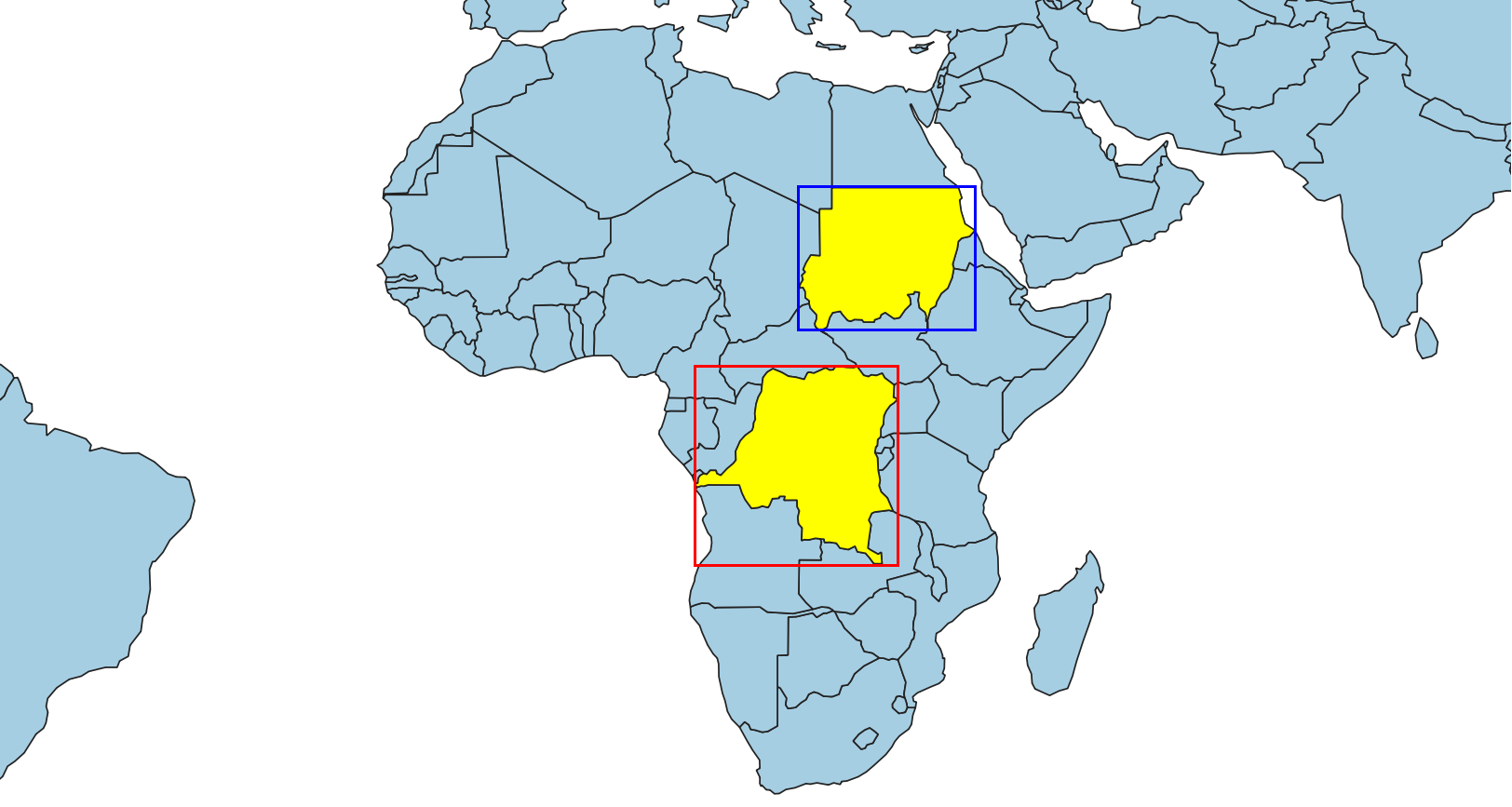
Figura 4.2 - Dois REM disjuntos implicam em duas geometrias disjuntas.

Obviamente que quando os REM possuem intersecção, podemos ter outros dois casos. O primeiro, ilustrado na Figura 4.3, mostra que apesar dos dois REM terem intersecção, não há garantias de que as respectivas geometrias tenham algum tipo de interação espacial. O caso mostrado na Figura 4.4, ilustra que se um par de geometrias possui intersecção, então seus REM também possuem.

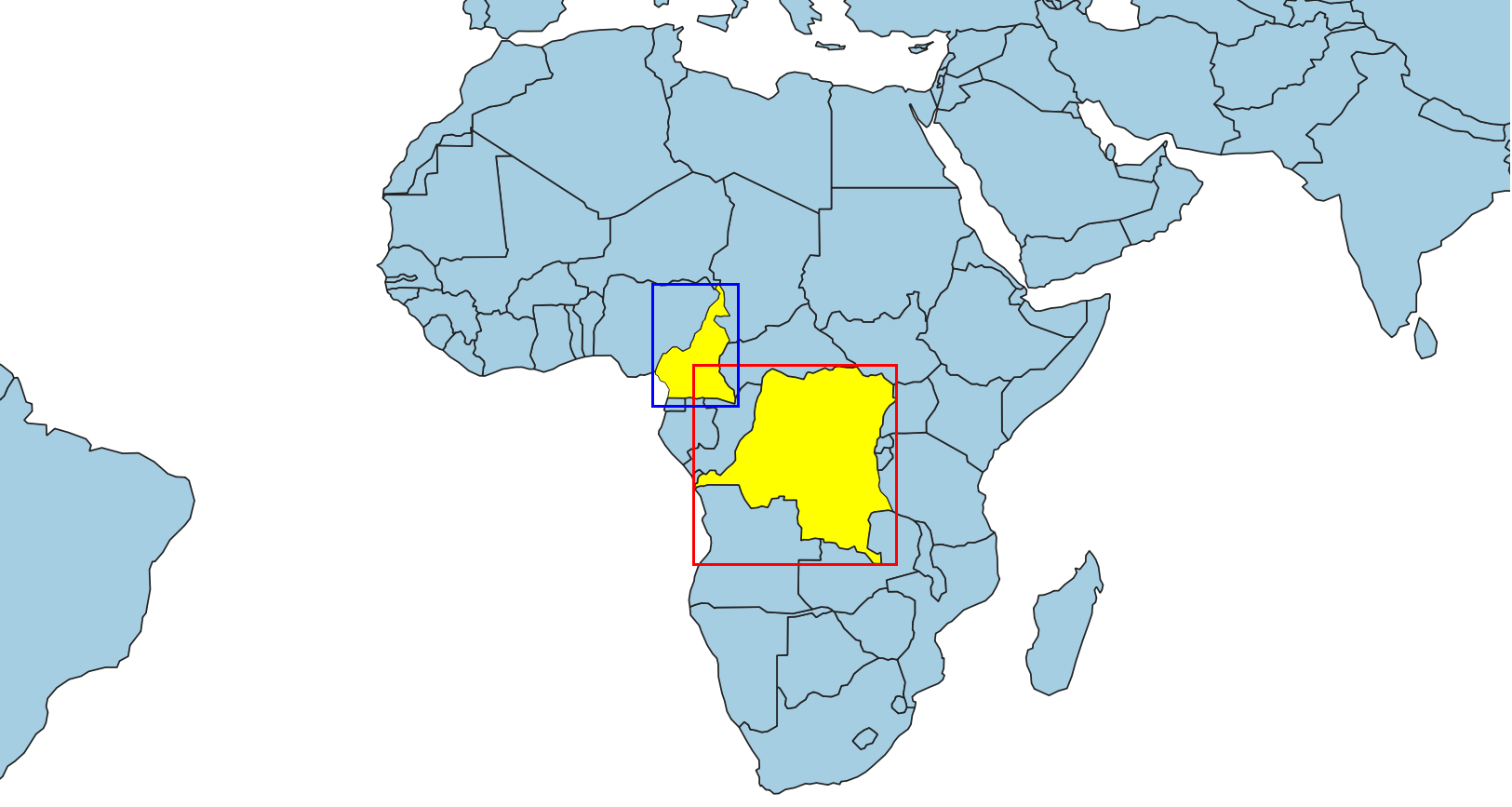
Figura 4.3 - Dois REM com intersecção não necessariamente implicam em duas geometrias com interação espacial.

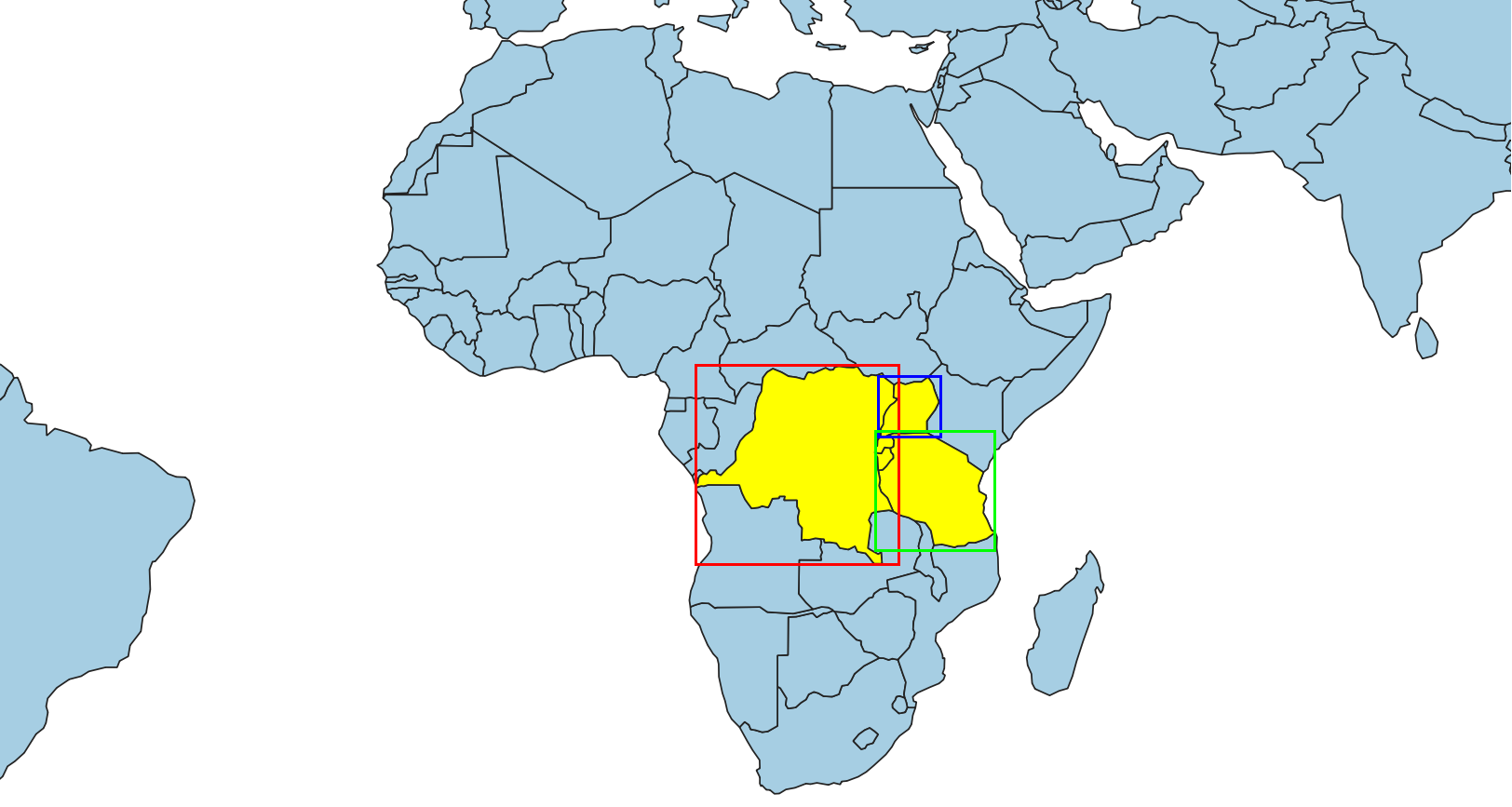
Figura 4.4 - Se duas geometrias possuem intersecção, então seus REM também terão intersecção.

A grande maioria dos métodos de indexação espacial são projetados sobre o MBR das geometrias. Afinal, seria muito complexo as chaves dos índices serem formadas ou representadas pelas geometrias exatas de elementos geométricos como linhas e polígonos. Além disso, os índices seriam extremamente custosos e proibitivos, com as geometrias exatas. Portanto, todos os SGBDs com suporte a tipos espaciais utilizam bastante as propriedades dos REM das geometrias para construção das estruturas de índices.