4.4. Árvores de Partição do Espaço
As Árvores-B e suas variantes, assim como as Árvore-R e suas variantes, e o GiST, dão suporte à classe de árvores balanceadas. Existe também uma classe de árvores denomina de Árvores de Partição do Espaço (Space-partitioning Trees) que particionam o espaço multidimensional em subregiões disjuntas. As Árvore-k-d [5] [6] e as Quad-trees [15] [37] se enquadram nessa classe de árvores.
Para ilustrar a idéia dessa classe de árvores, considere os 38 pontos mostrados na Figura 4.11, que representam os centróides de algumas das cidades da região do triângulo mineiro no Estado de Minas Gerais.
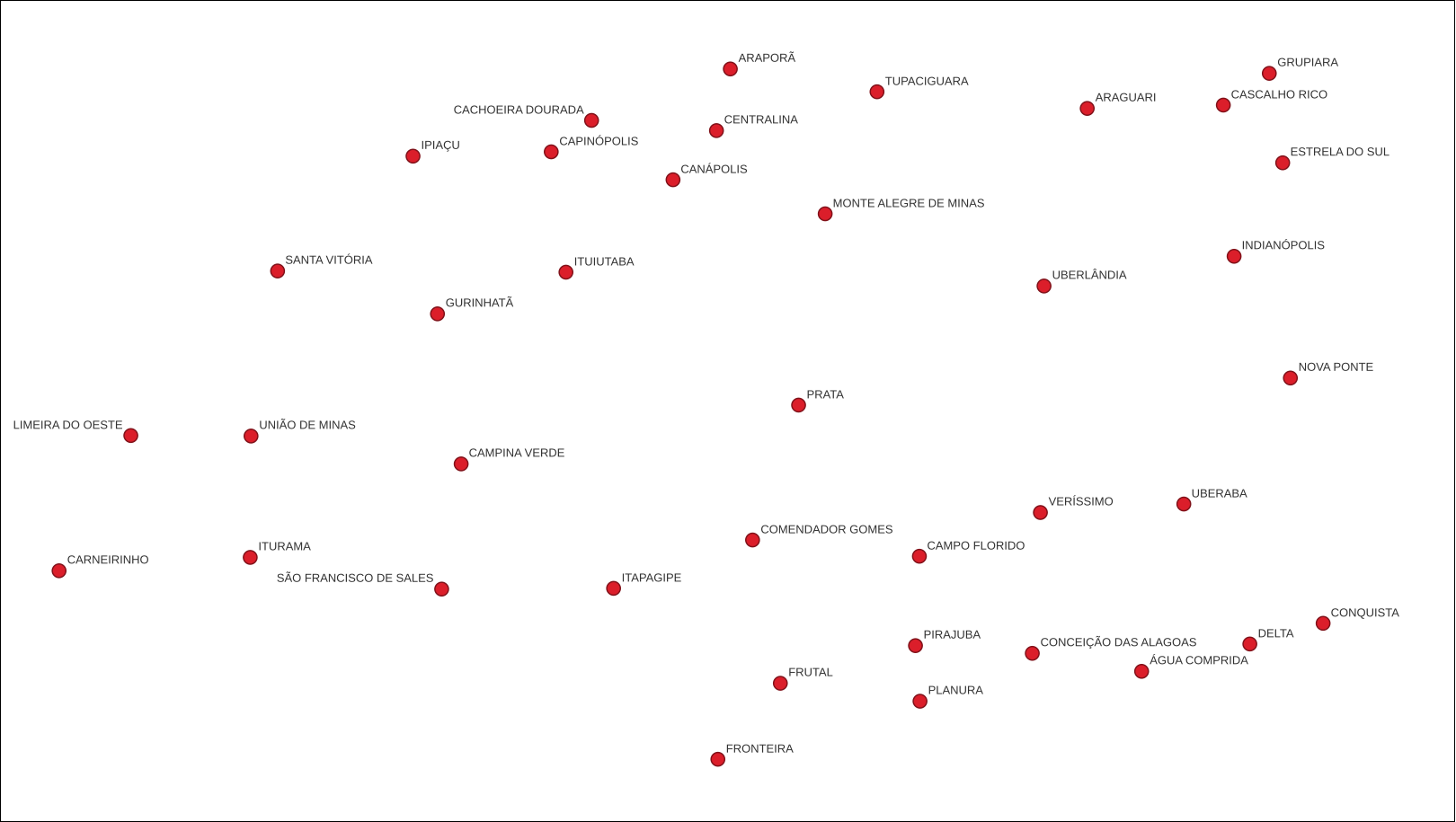
Figura 4.11 - Centróides de cidades do triângulo mineiro.
Uma possível forma de estruturarmos esses pontos para suportar consultas de retângulo (range query) ou janela (window query) seria através de uma Árvore-k-d. Uma Árvore-k-d é uma árvore binária, ou seja, cada nó interno possui no máximo dois descendentes, não importando a dimensionalidade \(k\) do espaço envolvido. Esta árvore foi proposta originalmente por Bentley em 1975 [5] como uma alternativa à solução de um problema mais genérico do que o geométrico, que é o de busca baseada em chaves com vários atributos.
A construção de uma Árvore-k-d é feita tomando-se de maneira alternada o valor ao longo de uma das dimensões do dado para particionar os conjuntos de elementos da sub-árvore esquerda e da sub-árvore direita. Na Figura 4.12, podemos observar que os valores das dimensões \(x\) e math:`y foram usadas alternadamente para estabelecer as partições.
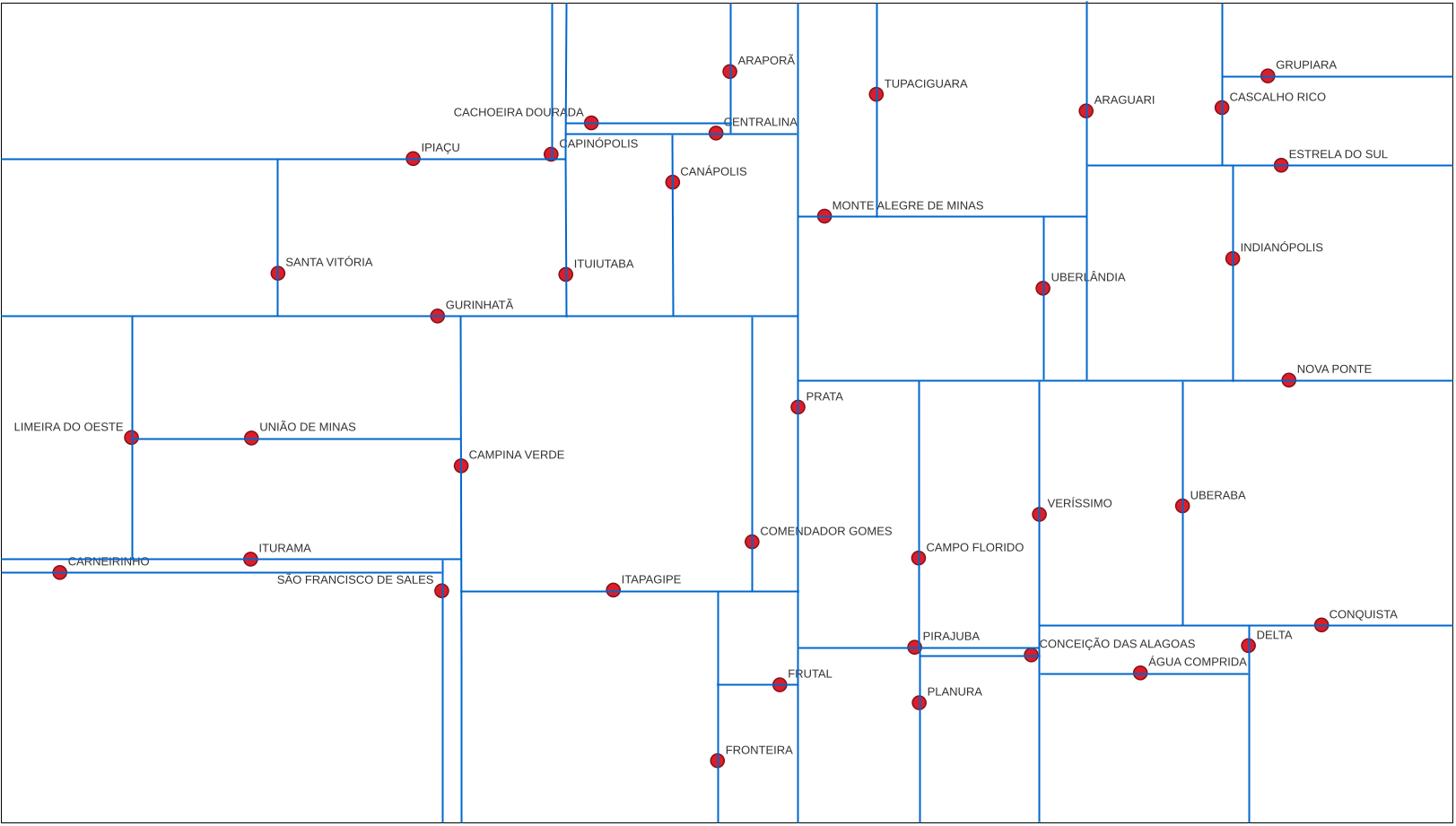
Figura 4.12 - Partição do espaço através de um Árvore-k-d.
A Figura 4.13 mostra a estrutura da Árvore-k-d para um espaço bidimensional. Repare que no primeiro nível da árvore a coordenda \(x\) da localização correspondente ao centróide da cidade PRATA divide o espaço em dois sub-conjuntos, as cidades à esquerda dessa coordenada e as cidades à direita. No segundo nível da árvore, a coordenda \(y\) das cidades de GURINHATÃ e NOVA PONTE, particionam novamente os seus respectivos sub-espaços em dois novos sub-espaços, com os sub-conjuntos de pontos acima e abaixo da coordenada \(y\) dessas cidades. Esse processo de partição é aplicado a todos os pontos do conjunto, produzindo a árvore da Figura 4.13 e as partições da Figura 4.12.
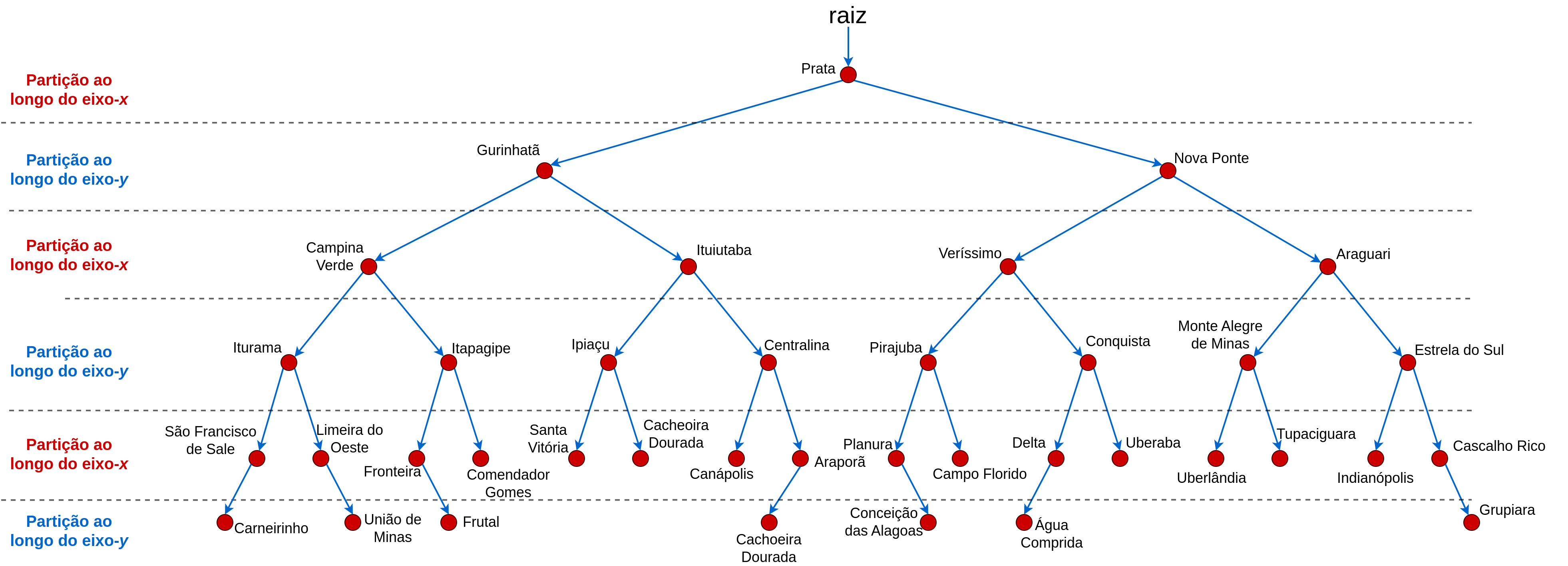
Figura 4.13 - Árvore-k-d.
Assim como as Árvores Binárias de Pesquisa, as Árvores-k-d são utilizadas para problemas que cabem completamente na memória principal (RAM), não sendo apropriadas como índices armazenados em meio secundário (disco). Existem variantes dessa estrutura que foram projetadas para permitir seu uso eficiente em meio secundário. A K-D-B-Tree é uma dessas variantes [35], mas no entanto não é muita utilizada na prática pelos atuais sistemas de bancos de dados.
Outro tipo de árvore importante pertencente a esta classe denomina de Árvores de Partição do Espaço são as Quad-trees [15]. Para uma revisão da literatura sobre essa estrutura, consulte [37].