4.2. Árvores-R

Uma Árvore-R é uma árvore balanceada, com uma estrutura semelhante a uma Árvore-B. Trata-se do método de indexação mais empregado na indústria de bancos de dados geoespaciais, estando presente em produtos como o Oracle Spatial, PostgreSQL/PostGIS e o MySQL.​

Considere o conjunto de retângulos mostrados na Figura 4.5. Esses retângulos, numerados de 1 a 20, podem representar, por exemplo, a aproximação geométrica de polígonos ou linhas poligonais.

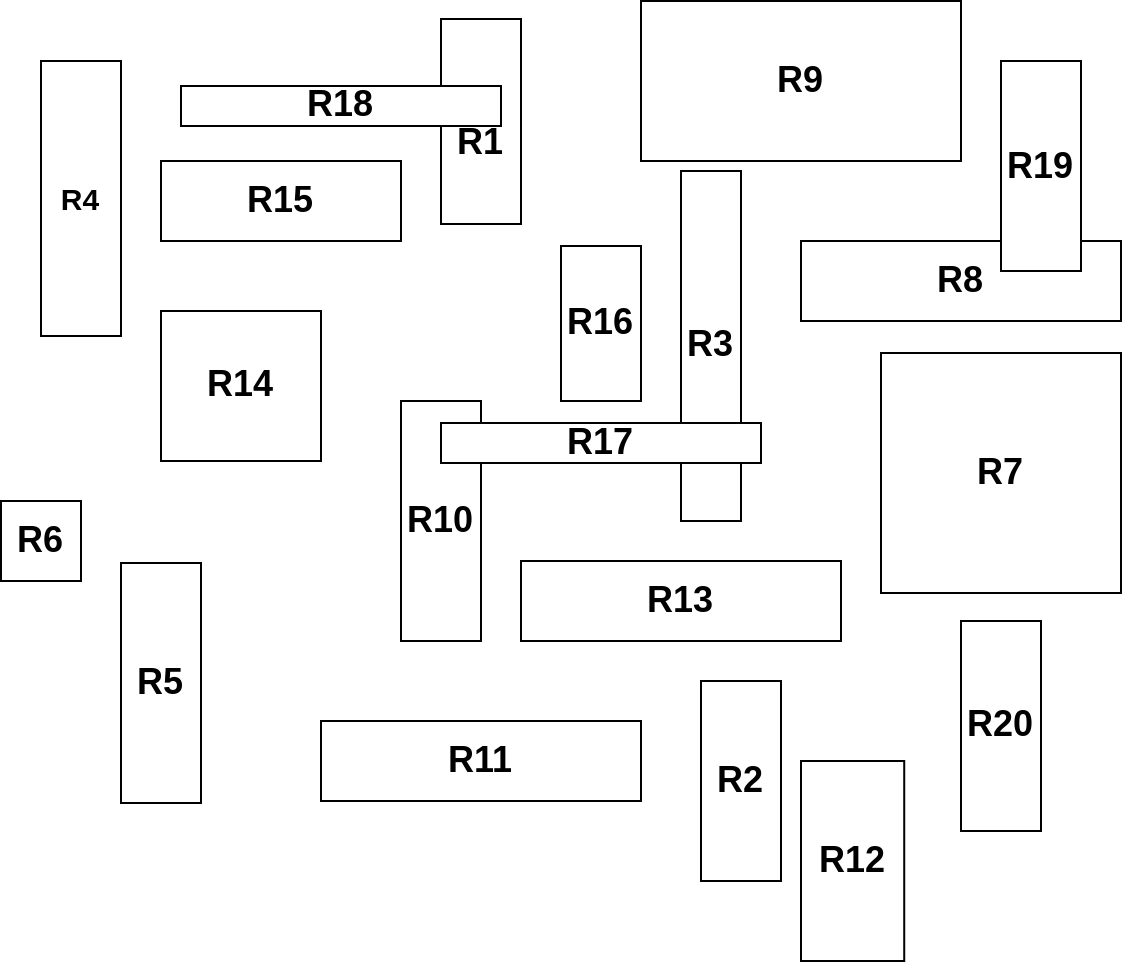
Figura 4.5 - Retângulos envolventes das geometrias indexadas.

Uma Árvore-R organiza o espaço subjacente em uma hierarquia de retângulos, possivelmente com sobreposições. A Árvore-R apresentada na Figura 4.6 ilustra uma hierarquia criada a partir dos retêngulos da Figura 4.5. Nessa árvore, os nós ou páginas internas são formados por entradas definidas por pares \((\text{retângulo}, \text{ponteiro-descendente})\). O retângulo de uma entrada contém os retângulos da sub-árvore indicada pelo ponteiro de ligação. Assim, o retângulo da entrada \(R_a\) contém os retângulos \(A\), \(B\) e \(G\), respectivamente, assim como todos os demais retângulos abaixo deles. As páginas no nível das folhas são formadas por entradas do tipo \((\text{retângulo}, \text{ponteiro-objeto})\), para que seja possível recuperar o objeto indexado. No nosso exemplo, esses retângulos estarão associados a geometrias de uma determinada coluna de uma tabela e, portanto, o índice conterá informações para que a linha possa ser recuperada (TID é a abreviação de tuple identifier).

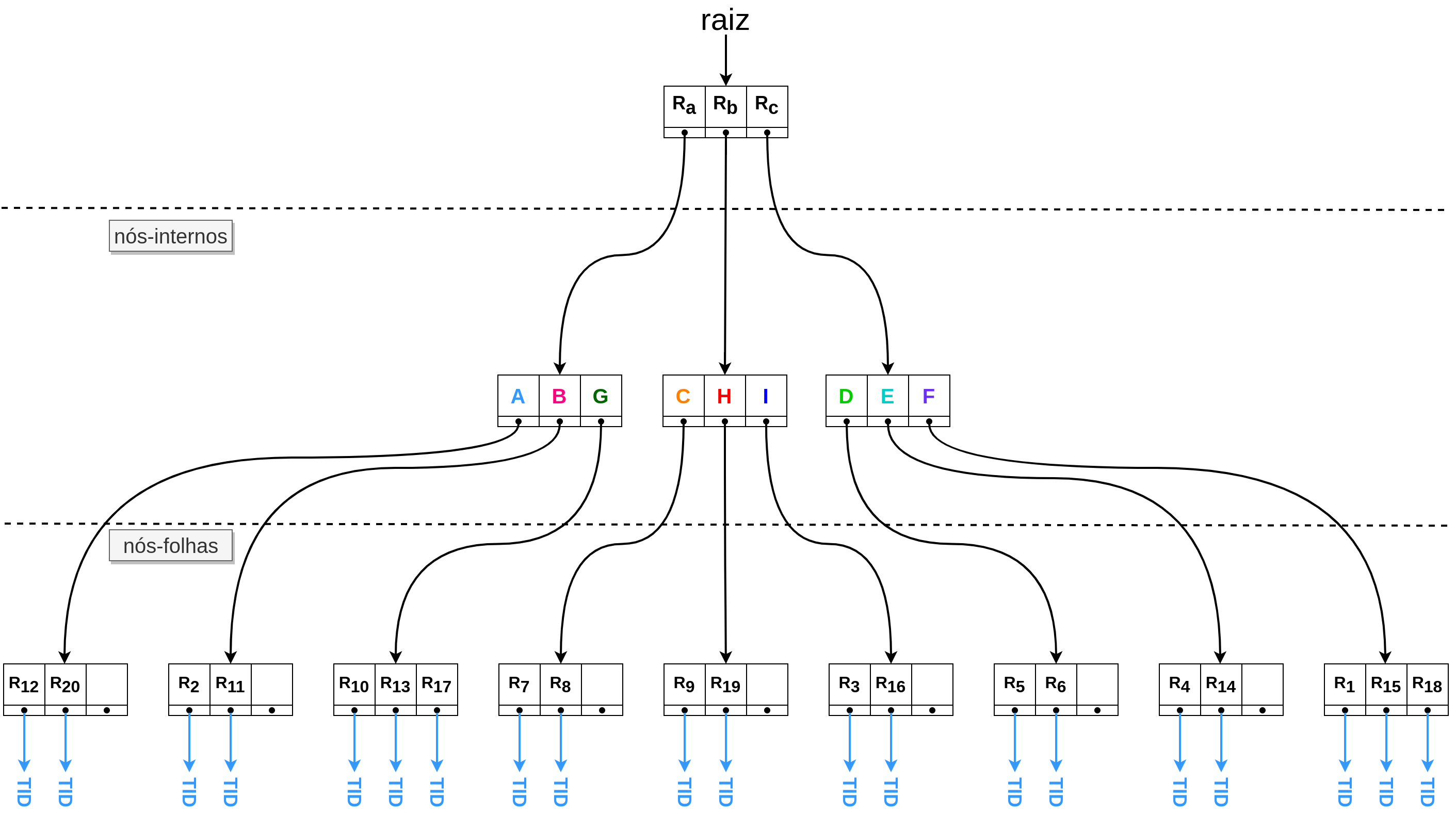
Figura 4.6 - Esquema de uma Árvore-R.

As Figuras 4.7 e 4.8 ilustram a hierarquia de retêngulos definida pela árvore mostrada acima.

Figura 4.7 - Retângulos do nó raiz e seus descendentes diretos.

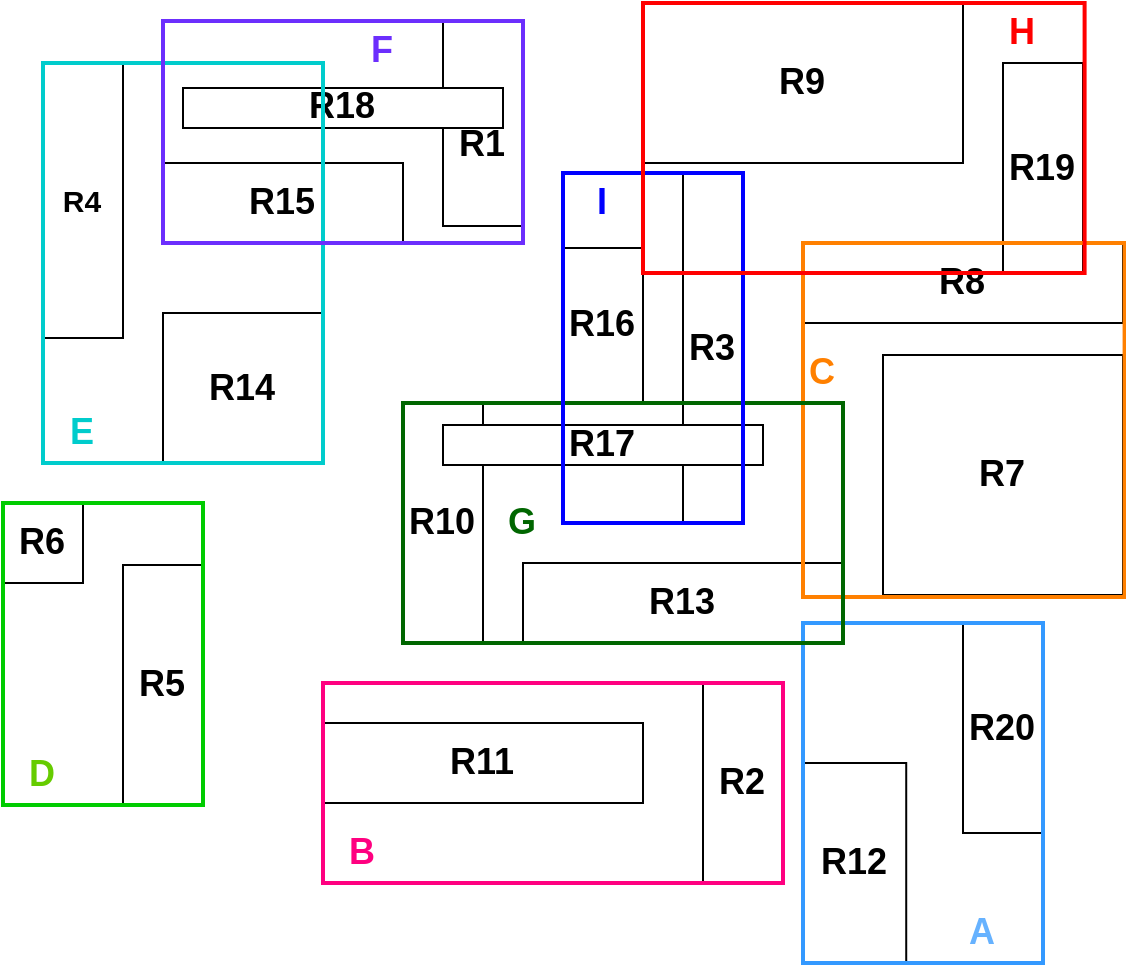
Figura 4.8 - Hierarquia dos retângulos dos nós internos e das folhas.

Uma Árvore-R deve satisfazer as seguintes propriedades:

• O número máximo de entradas em uma página é dado por \(M\).

• O número mínimo de entradas em uma página é definido como \(m = \lceil \frac{M}{2} \rceil\). Esse parâmetro é responsável pelo balanceamento da árvore.

• Toda página contém entre \(m\) e \(M\) entradas válidas. A única exceção é o nó raiz.

• Se a árvore tiver mais do que um nível, isto é, pelo menos \(altura = 1\), a raiz terá ao menos dois descendentes.

• Para cada entrada dos nós internos, que são formados por entradas representadas pelos pares \((\text{retângulo}, \text{ponteiro-descendente})\), o \(retângulo\) dessa entrada será o menor retângulo a conter todos os retângulos das entradas do nó descendente. Repare nas figuras acima, que o retângulo \(R_a\) contém os retângulos \(A\), \(B\) e \(G\). Por sua vez, o retângulo \(G\) contém os retângulos \(R_{10}\), \(R_{13}\) e \(R_{17}\).

• Para cada entrada dos nós folhas, que são formados por entradas representadas pelos pares \((\text{retângulo}, \text{ponteiro-objeto})\), o \(retângulo\) dessa entrada será o retângulo envolvente do objeto indexado.

• Todas as folhas encontram-se no mesmo nível.

• A altura \(h\) de uma Árvore-R indexando \(n\) objetos espaciais é: \(h \leqslant (\log_m n) - 1\).

4.2.1. Realizando Buscas numa Árvore-R

Considere uma pesquisa por objetos de uma tabela cujo retângulo envolvente possui algum tipo de interação com o retângulo de busca destacado em vermelho na Figura 4.9. A busca em uma Árvore-R começa sempre pelo nó raiz (Figura 4.6). No nó raiz, o retângulo de busca intercepta o retângulo da entrada \(R_a\). Assim, a busca terá que verificar a sub-árvore indicada pelo ponteiro de ligação associado ao retângulo \(R_a\). Ao verificar o nó de entradas \(\{A, B, G\}\), apenas o retângulo \(A\) é interceptado pelo retângulo de busca. Portanto, a busca seguirá a sub-árvore indicada pelo ponteiro de ligação associado ao retângulo \(A\). Ao chegar no nó folha, com as entradas de retângulos \(\{R_{12}, R_{20}\}\), todas as entradas devem ser verificadas e aquelas cujo retângulo tiverem interseção com o retângulo de busca devem ser reportadas. Portanto, apenas o TID associado ao retângulo \(R{20}\) será reportado nessa busca.

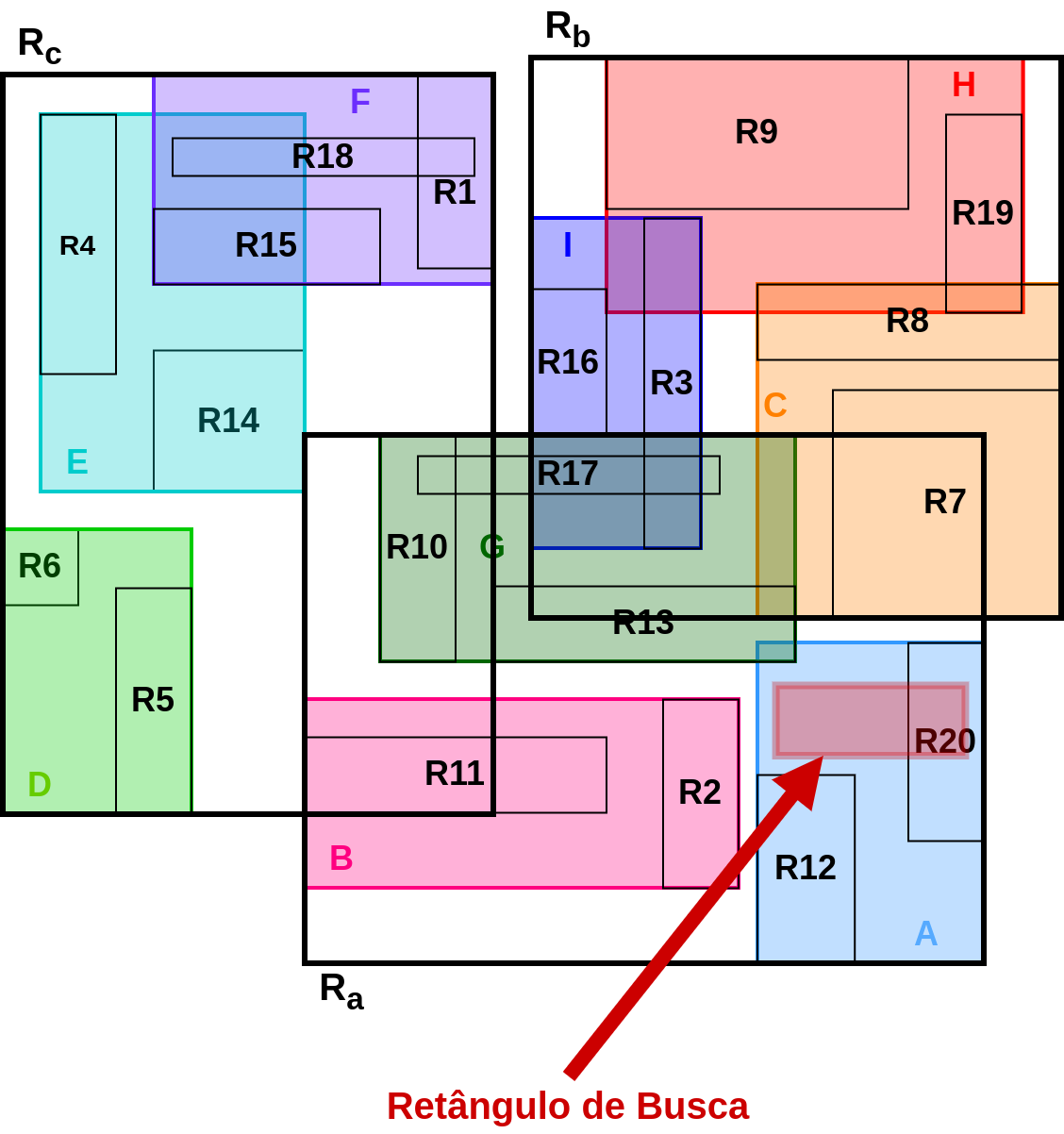
Figura 4.9 - Pesquisa em Árvores-R.

Agora, considere o novo retângulo de busca mostrado na Figura 4.10. Partindo do nó raiz (Figura 4.6), podemos observar que esse novo retângulo intercepta os retângulos \(R_a\) e \(R_c\). Aqui começa a primeira diferença em relação às Árvores-B. Uma busca pode seguir mais de um caminho da raiz até os nós folhas. Nesse exemplo, será necessário verificar tanto a sub-árvore associada à entrada \(R_a\) quanto a sub-árvore associada à entrada \(R_c\). No nó filho da entrada de retângulo \(R_a\), nenhum dos retângulos (\(\{A, B, G\}\)) das entradas possui interseção e, logo, não será preciso verificar mais nenhum caminho abaixo desse nó. No entanto, a busca ainda precisa verificar o nó filho da entrada de retângulo \(R_c\). Nesse nó, o retângulo de busca intercepta os retângulos das entradas \(D\) e \(E\). Novamente, as sub-árvores dessas duas entradas precisarão ser verificadas. Chegando aos dois nós folhas, os valores de TID das entradas \(\{R_5, R_4, R_{14}\}\) serão reportados.

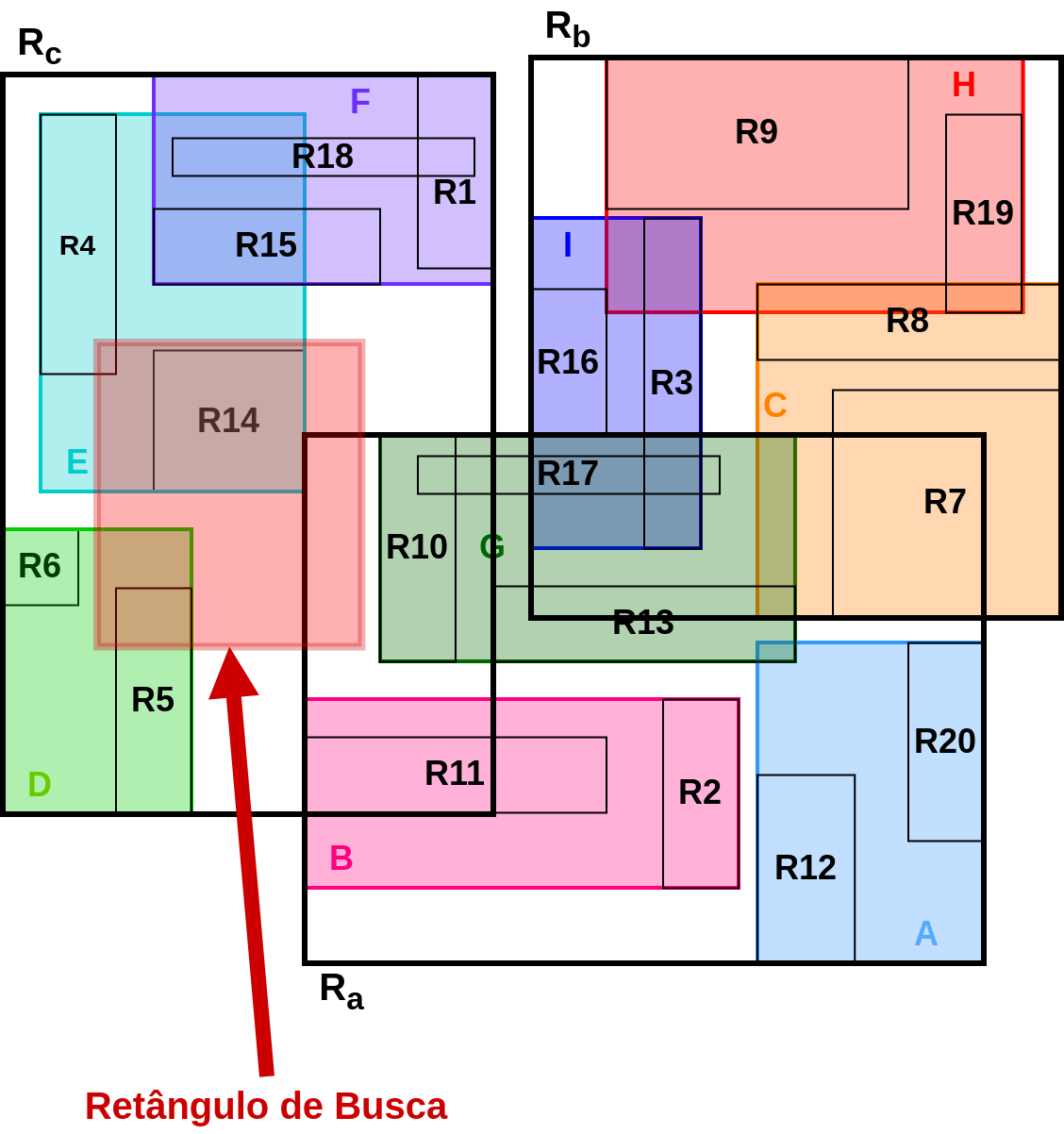
Figura 4.10 - Pesquisa em Árvores-R.

Os algoritmos de busca realizam uma travessia na Árvore-R a partir da raiz, de forma similar a uma Árvore-B. No entanto, diferentemente de uma Árvore-B, mais de um caminho ou sub-árvore de um nó pode ter que ser visitado, o que não garante um bom desempenho no pior caso. No entanto, é esperado que os algoritmos de atualização mantenham a árvore com uma forma que possibilite eliminar regiões irrelevantes nas buscas.

Nota

O fato de um retângulo de busca poder interceptar mais de um retângulo no mesmo nó, faz com que a busca possa ter que pesquisar em vários caminhos da raiz até as folhas.