2.23. Índices - Estruturas de Acesso

Muitas vezes, as aplicações que trabalham com bancos de dados são projetadas de maneira a manipular apenas uma fração dos dados desse banco. As aplicações OLTP (Online Transaction Processing), por exemplo, possuem esta característica. Consequentemente, ter apenas os arquivos das tabelas do banco de dados organizados em linhas armazenadas sequencialmente, sem uma forma de localizar rapidamente uma linha ou conjunto de linhas dependendo do valor de um determinado campo, pode acarretar em problemas de desempenho, principalmente, quando temos tabelas com muitas linhas e com volumes de dados que não são comportados em memória principal. Logo, estruturas de dados auxiliares que ajudem a localizar rapidamente uma linha ou um subconjunto das linhas de uma tabela, são imprescindíveis para um SGBD.

Vamos retomar a tabela municipio criada no Exercício 1 da Seção 2.22 - Importando e Exportando Dados. Essa tabela contém 5.570 linhas e possui a seguinte definição:

CREATE TABLE municipio
(
    id   CHAR(7) PRIMARY KEY NOT NULL,
    nome VARCHAR(40) NOT NULL
);

Em um SGBD relacional, como o PostgreSQL, o fato de definir uma ou mais colunas como chave primária, faz com que o SGBD tenha que verificar o valor desses campos nas operações de inserção (INSERT) e atualização (UPDATE). Essa verificação depende de um acesso rápido às linhas da tabela para identificar se o valor de chave primária fornecido na operação já existe na tabela. Como as operações de inserção, remoção e atualização podem fazer com que as linhas da tabela não respeitem a ordem da chave primária, é necessária uma estrutura de dados auxiliar que ajude a localizar rapidamente uma linha que contenha a chave primária. Por isso, o PostgreSQL cria automaticamente um índice associado às colunas que compõem a chave primária. Este é o caso da coluna id da tabela municipio, conforme mostrado na descrição dessa tabela pelo aplicativo psql:

\d municipio

Saída:

                    Table "public.municipio"
 Column |         Type          | Collation | Nullable | Default
--------+-----------------------+-----------+----------+---------
 id     | character(7)          |           | not null |
 nome   | character varying(40) |           | not null |
Indexes:
    "municipio_pkey" PRIMARY KEY, btree (id)

Repare na saída acima que um índice denominado municipio_pkey foi criado, associado à coluna id que é chave primária. A saída acima também indica que esse índice é do tipo btree. Mais adiante neste capítulo, será discutido os vários tipos de índices e suas aplicações. Por hora, vamos compreender como o PostgreSQL executa uma consulta envolvendo a busca por um valor de chave primária. O comando EXPLAIN do PostgreSQL junto à opção ANALYZE apresenta o plano a ser usado na execução de uma consulta. O comando abaixo exibe como o PostgreSQL irá recuperar a linha com id de valor 2112704:

EXPLAIN (ANALYZE TRUE, FORMAT YAML)
    SELECT * FROM municipio WHERE id = '2112704';

Saída:

                 QUERY PLAN
--------------------------------------------
 - Plan:                                   +
     Node Type: "Index Scan"               +
     Parallel Aware: false                 +
     Async Capable: false                  +
     Scan Direction: "Forward"             +
     Index Name: "municipio_pkey"          +
     Relation Name: "municipio"            +
     Alias: "municipio"                    +
     Startup Cost: 0.28                    +
     Total Cost: 8.30                      +
     Plan Rows: 1                          +
     Plan Width: 21                        +
     Actual Startup Time: 0.038            +
     Actual Total Time: 0.041              +
     Actual Rows: 1                        +
     Actual Loops: 1                       +
     Index Cond: "(id = '2112704'::bpchar)"+
     Rows Removed by Index Recheck: 0      +
   Planning Time: 0.142                    +
   Triggers:                               +
   Execution Time: 0.074
(1 row)

As linhas destacadas na saída acima indicam que o PostgreSQL irá utilizar uma estratégia de consulta baseada no índice municipio_pkey associado à coluna id. Essa estratégia faz com que o PostgreSQL seja muito eficiente na busca da linha procurada.

Vamos agora verificar como o PostgreSQL trata uma consulta aonde ele não poderá contar com um índice auxiliar. Para isso, vamos construir uma consulta nessa mesma tabela que recupere a linha do município de nome Araxá:

EXPLAIN (ANALYZE TRUE, FORMAT YAML)
    SELECT * FROM municipio WHERE nome = 'Araxá';

Saída:

                 QUERY PLAN
----------------------------------------------
 - Plan:                                     +
     Node Type: "Seq Scan"                   +
     Parallel Aware: false                   +
     Async Capable: false                    +
     Relation Name: "municipio"              +
     Alias: "municipio"                      +
     Startup Cost: 0.00                      +
     Total Cost: 105.62                      +
     Plan Rows: 1                            +
     Plan Width: 21                          +
     Actual Startup Time: 1.341              +
     Actual Total Time: 3.603                +
     Actual Rows: 1                          +
     Actual Loops: 1                         +
     Filter: "((nome)::text = 'Araxá'::text)"+
     Rows Removed by Filter: 5569            +
   Planning Time: 0.195                      +
   Triggers:                                 +
   Execution Time: 3.637
(1 row)

Nesse caso, sem uma estrutura de dados auxiliar, o SGBD precisará verificar todas as linhas da tabela municipio para localizar a linha ou linhas que possuem o valor Araxá no campo nome. As linhas destacadas na saída acima mostram que o PostgreSQL irá varrer os registros da tabela de maneira sequencial e que por isso, 5.569 linhas serão verificadas e descartadas, para resultar apenas na linha de Araxá. Portanto, os índices são usados justamente para evitar esse tipo de situação. Ao definir um índice sobre a coluna nome, a estrutura de dados auxiliar criada possibilitará ao SGDB localizar a linha ou linhas de interesse sem a necessidade de realizar a leitura de toda a tabela.

A existência de estruturas de dados ou índices bem projetados nos SGBDs é fundamental para minimizar o acesso a disco. Ainda hoje, muitos sistemas de bancos de dados operam com conjuntos de discos mecânicos que possuem um esquema semelhante ao mostrado na Figura 2.31. Portanto, um dos objetivos dos SGBDs é diminuir a quantidade de operações de leitura realizadas entre esse tipo de equipamento e a memória RAM, onde os dados são mantidos para posterior operação.

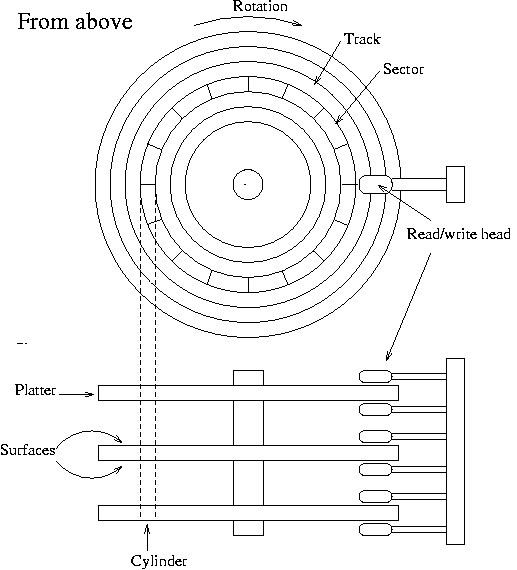
Figura 2.31 - Figura esquemática de um disco rígido mecânico.
Fonte: Wirzenius et al. [41].

Existem dois conjuntos de métodos bem consolidados na literatura que são usados pelos SGBDs para indexar dados: as funções hash e as estruturas de dados conhecidas por árvores. Nessa seção iremos examinar os fundamentos desses métodos bem como a criação de índices no PostgreSQL para os tipos de dados básicos (números inteiros e reais, strings, data e hora) e mais adiante no curso, retomaremos essa discussão com os tipos JSON e PostGIS Geometry.

2.23.1. Funções Hash

EM DESENVOLVIMENTO

2.23.2. Árvores

Definição: Uma árvore é definida como um conjunto finito de um ou mais nós (em Inglês, nodes), sendo um deles designado raiz (em Inglês, root node), e os demais elementos, particionados em \(k \geqslant 0\) conjuntos disjuntos, \(T_1, ..., T_k\), em que cada um desses conjuntos também são árvores [22]. A Figura 2.32 ilustra essa definição.

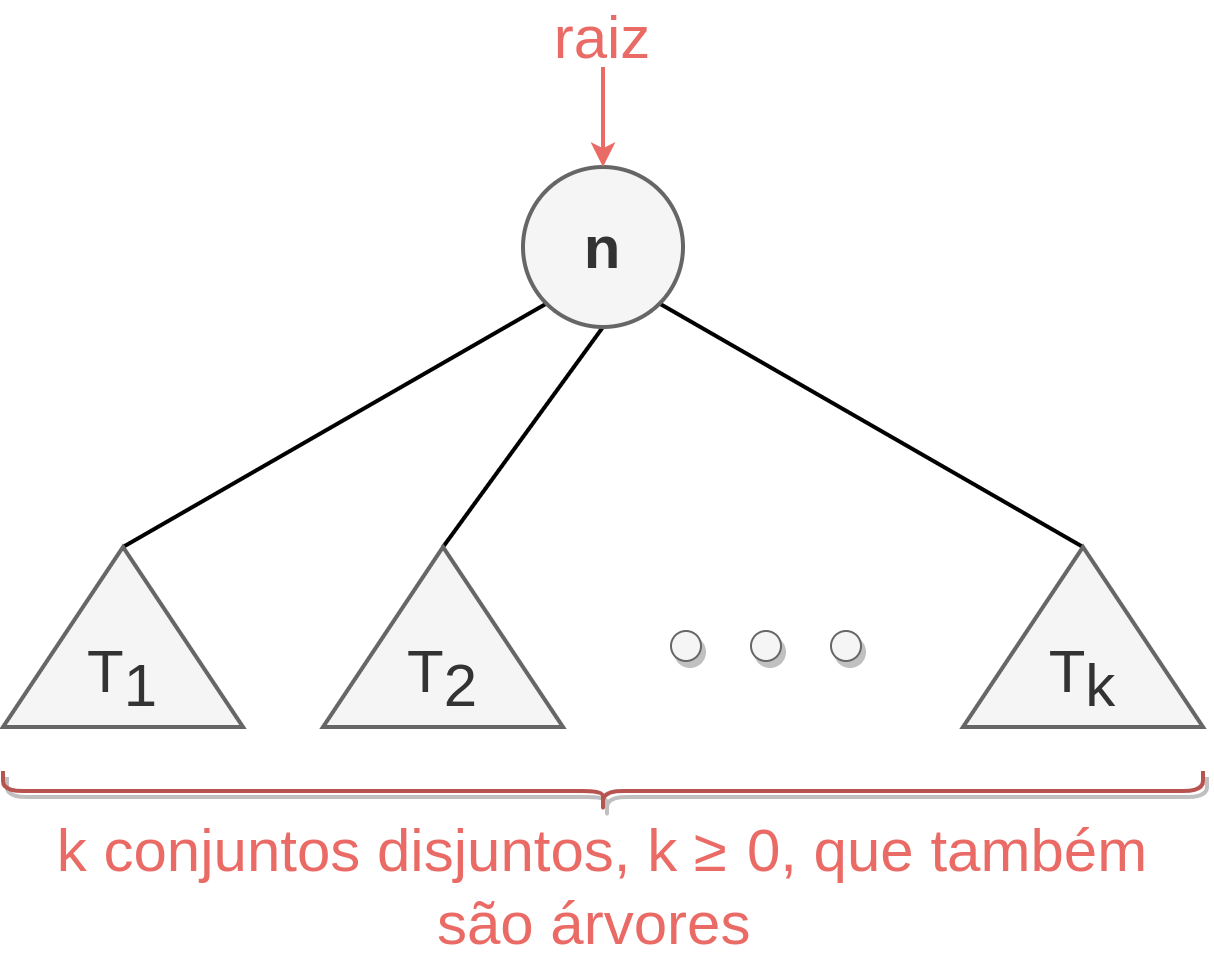
Figura 2.32 - Definição de árvores com raiz.

Pela definição acima, a estrutura de dados árvore é uma estrutura recursiva pois cada um dos conjuntos \(T_i\), com \(1 \leqslant i \leqslant k\), também são árvores.

2.23.2.1. Árvores Binárias de Pesquisa​

A Figura 2.33 apresenta uma estrutura conhecida por árvore binária de pesquisa (em Inglês, binary search tree).

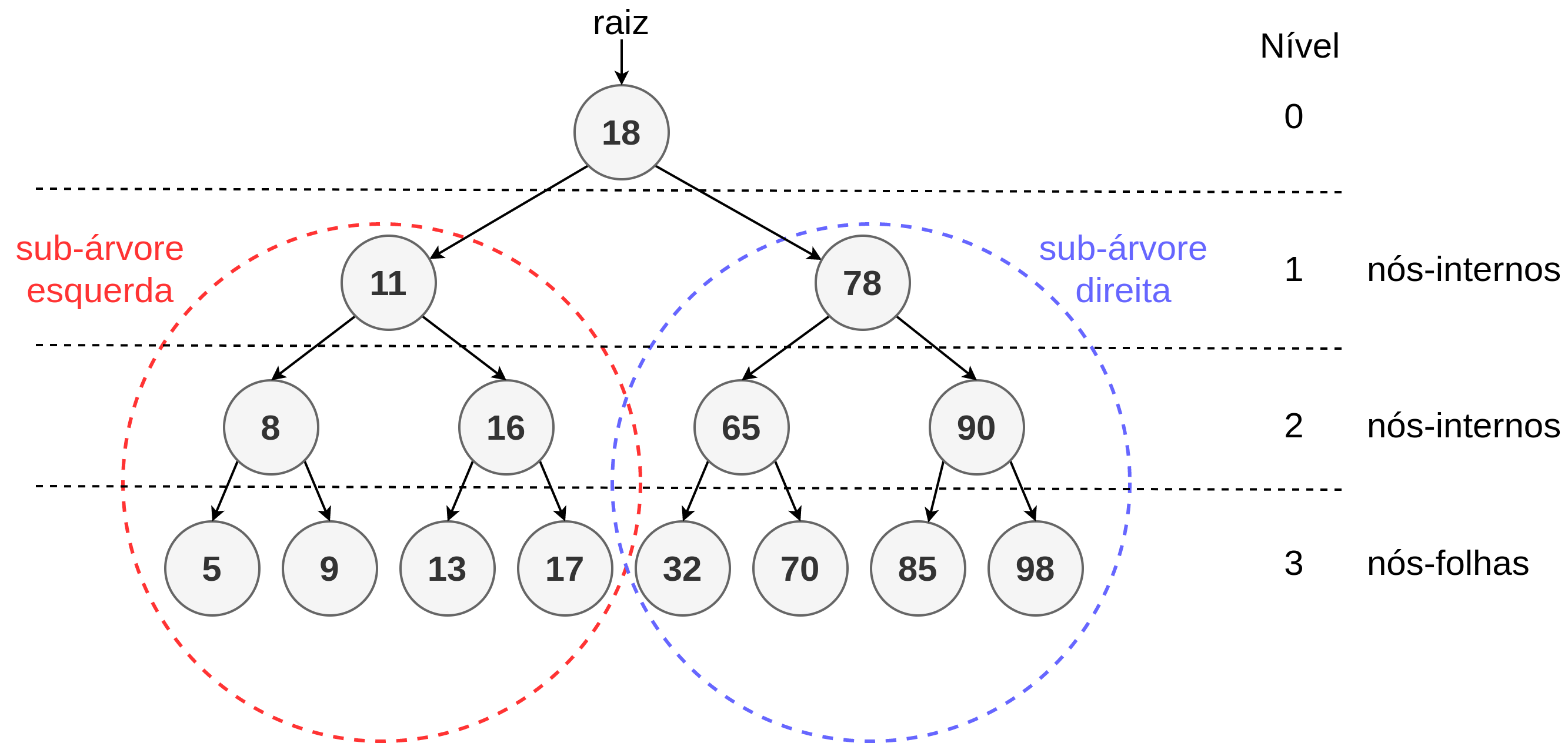
Figura 2.33 - Árvore Binária de Pesquisa.

​Numa árvore binária de pesquisa, os nós possuem chave única, isto é, não há valores duplicados de chave. O nó superior é denominado raiz da árvore. Na figura, o nó com chave de valor 18 é a raiz dessa árvore. Os nós à esquerda do nó raiz formam a sub-árvore esquerda, enquanto os nós à direita, formam a sub-árvore direita. Os valores de chave da sub-árvore esquerda são menores que as da sub-árvore direita. As chaves da sub-árvore esquerda são menores do que a da raiz. As chaves da sub-árvore direita são maiores do que a da raiz. As sub-árvores esquerda e direita também são árvores binárias de pesquisa. Repare que o nó com chave de valor 11 pode ser visto como a raiz de uma nova árvore e que a relação entre os valores de chave (à esquerda dos nós e à direita dos nós) são preservados nessa sub-árvore.

Essa estrutura permite realizar buscas por valores de chave muito facilmente e, se bem estruturada, de forma eficiente. Suponha que estejamos procurando a chave 70. Começamos a busca pela raiz da árvore, que possui o valor 18. Como o valor procurado é maior que a chave 18, os nós da sub-árvore esquerda não precisarão ser pesquisados, uma vez que todos os valores​ de chave dessa sub-árvore também serão menores que 18. Assim, a busca continua no nó à direita da raiz, que possui chave de valor 78. Como a chave procurada é menor que 78, podemos descartar todos os nós da sub-árvore à direita do nó 78, concentrando a busca na sub-árvore esquerda, que possui o nó com valor de chave 65. Como a chave procurada é maior que 65, tomamos o caminho da sub-árvore direita, chegando ao nó de chave 70, que é igual ao valor procurado e, assim, nossa busca termina com sucesso. Em resumo, a busca pela chave 70 nos levou a examinar os nós \(\{18, 78, 65, 70\}\). Isso significa que a busca em uma árvore binária de pesquisa depende, essencialmente, da altura ou profundidade dela.

Numa estrutura de árvore binária de pesquisa como a da Figura 2.33, temos as seguintes definições:

• Os elementos indicados por círculos são denominados nós. Nessa árvore temos, portanto, 15 nós.

• Os valores apresentados dentro de cada nó são denominados de chave (em Inglês, key).

• O grau de um nó é definido como o número de sub-árvores deste nó. Nessa figura, o grau do nó de chave 18 é 2, isto é, ele possui dois descendentes diretos. O grau do nó de chave 5 é 0, isto é, ele não possui descedentes.

• O grau máximo numa árvore binária é dois. Portanto, podemos ter nós com zero, um ou dois descendentes.

• Os nós que não possuem descendentes são denominados folha (em Inglês, leaf node) ou terminais (em Inglês, terminal). Na figura, os nós \(\{5, 9, 13, 17, 32, 70, 85, 98\}\) são folha.

• Os nós que não são folha, são chamados de internos ou não-terminais. Os nós de chave \(\{11, 78, 8, 16, 65, 90\}\) são considerados nós internos ou nós não-terminais.

• Os nós que são raízes das sub-árvores de um nó \(x\) da árvore, são chamados de filhos (em Inglês, children nodes) do nó \(x\). Por exemplo, os elementos filhos do nó de chave 78 são: \(\{65, 90\}\). O nó \(x\) é pai (em Inglês, parent node) de seus filhos.​ Por exemplo, o nó pai do nó de chave 90 é o nó de chave 78.

• Os nós filhos de um mesmo nó são chamados de irmãos (em Inglês, sibling nodes).

• Os ancestrais de um nó (em Inglês, ancestors) são todos os nós no caminho da raiz até o nó em questão. Por exemplo, os ancestrais do nó com chave 70 são: \(\{18, 78, 65\}\).

• O nível de um nó é definido tomando a raiz como nível 0. Se um nó encontra-se no nível \(i\), seus filhos encontram-se no nível \(i + 1\).​

• A altura (height) ou profundidade (depth) de uma árvore é o maior nível de qualquer nó dessa árvore.​ Existem duas convenções para se definir a altura de uma árvore binária: (a) o número de nós no maior caminho da raiz até a folha mais profunda; (b)​ o número de arestas no caminho mais comprido da raiz até a folha. Na Figura 2.33 ​adotamos a segunda convenção, isto é, o número de arestas no caminho mais comprido da raiz até a. Portanto, a árvore mostrada nessa figura possui altura 3.

• A árvore da Figura 2.33 é uma árvore binária plena ou árvore binária cheia pois todas as folhas encontram-se no mesmo nível. Repare que tanto a raiz quanto todos os nós internos possuem dois filhos.

Essa estrutura de dados nos permite estabelecer algumas fórmulas e propriedades interessantes:

• ​O número máximo de nós no nível \(i\) é \(2^{i}\), \(i \geq 0\). Desta forma, o nível 0 (a raiz) terá no máximo 1 nó. O nível 1 terá 2 nós. O nível 2 terá 4 nós. O nível 3 terá 8 nós. Se tivermos uma árvore de altura 10, no último nível, isto é, o nível 9, teremos no máximo 512 nós.

• O número máximo de nós \(n\) de uma árvore binária de altura \(h\) é dado por: \(n = \sum_{i=0}^{h} 2^{i}\), ou seja, \(n = 2^{h + 1} - 1, h \geq 0\). Na árvore da Figura 2.33, temos altura 3 e, logo, \(n = 2^4 - 1 = 15\ nós\).

• A altura de uma árvore binária plena com \(n\) nós é: \(h = \log_2(n + 1) - 1\), com \(n \geq 1\).

• Se uma árvore plena possui \(n\) nós na folha, o nível \(i\) das folhas será dado por​ \(i = (\log_2 n)\). Na árvore da Figura 2.33, temos 8 nós folha, logo, o nível será dados por \(\log_2 8 = \log_2 2^3 = 3\).

2.23.2.2. Árvores Balanceadas

As árvores binárias de pesquisa com altura \(O(\log_2n)\) são conhecidas como árvores balanceadas. Compare as árvores das Figuras 2.33 e 2.34. As duas árvores possuem 15 elementos com os mesmos valores de chave. No entanto, a árvore da Figura 2.34 é considerada desbalanceada pois as folhas estão presentes em níveis muito diversos da árvore. Um dos efeitos do desbalanceamento é produzir uma estrutura mais profunda e sem a garantia de que o caminho até todas as folhas tenham o mesmo comprimento, isto é, o mesmo número de nós. Veja o exemplo do nó folha com chave 90 que aparece no nível 3 e o nó folha com chave 65 que aparece no nível 6.

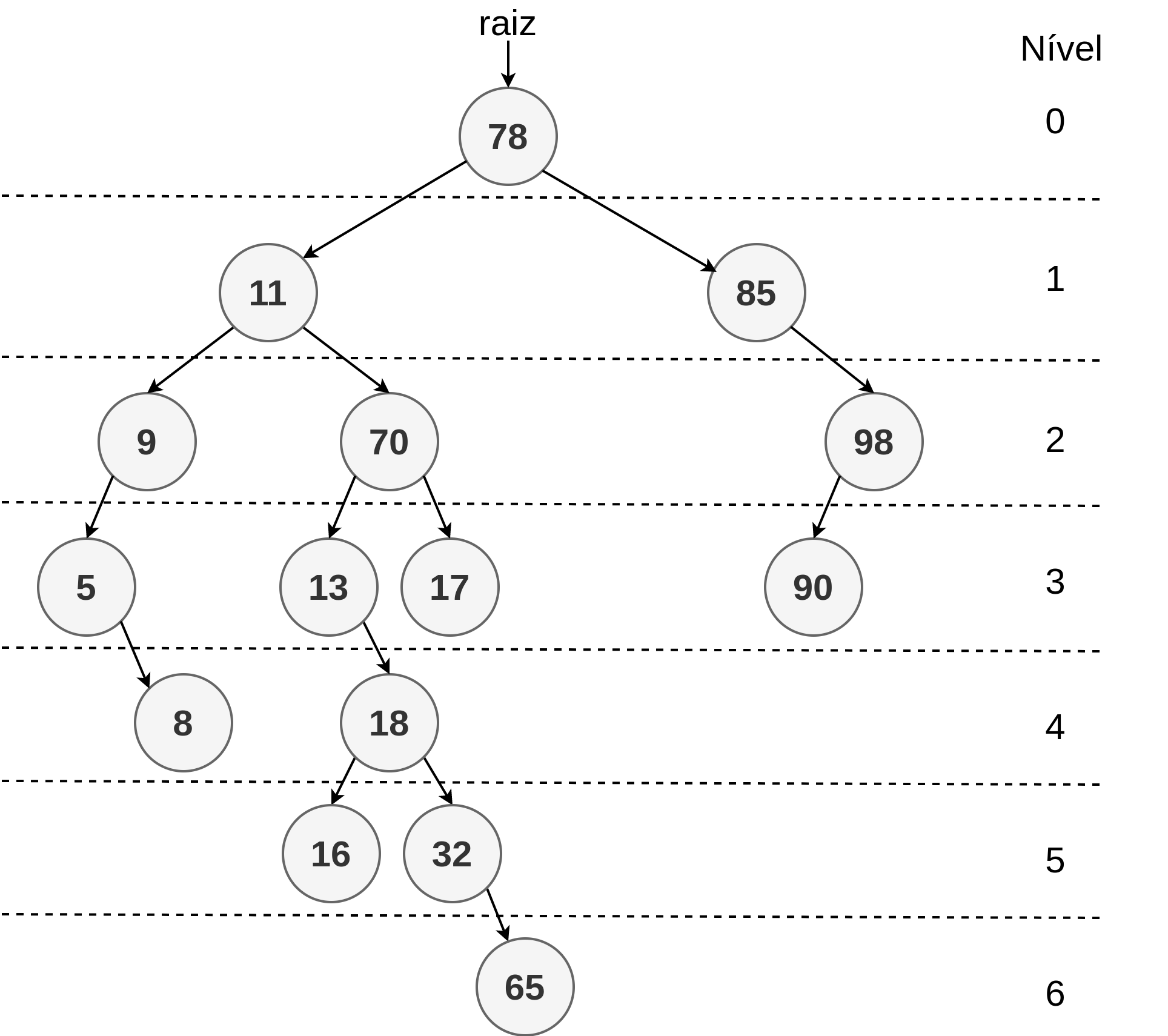
Figura 2.34 - Árvore Binária de Pesquisa desbalanceada.

​ É provado na literatura, que as árvores binárias de pesquisa criadas com inserções e remoções aleatórias tendem a produzir uma árvore de altura \(O(\log_2n)\) [1]. No entanto, para que isso seja uma garantia de fato, foram desenvolvidos vários métodos para manter uma árvore balanceada à medida que as operações de inserção e remoção são realizadas. As árvores binárias conhecidas por AVL​, Red-Black​ (árvores rubro-negras) e Splay-trees (ou zig-zag)​ são exemplos de árvores binárias de pesquisa balanceadas. Desta forma, as operações de busca, inserção e remoção são garantidamente realizadas em tempo logaritmico, ou seja, \(O(\log_2n)\).

Nota

De tudo que foi exposto acima, podemos concluir que a complexidade de realizar uma busca em uma árvore binária de pesquisa depende da altura \(h\) dessa árvore. Logo, se a árvore binária de pesquisa for balanceada e possuir \(n\) nós (ou elementos), a busca terá complexidade da ordem de​ \(O(\log_2n)\) pois \(h = \log_2(n + 1) - 1\).

Nota

As árvores são uma das estruturas de dados mais versáteis na computação, com ampla aplicação nos SGBDs e nas aplicações do dia-a-dia.

2.23.2.3. Árvores-B

As árvores binárias são usadas, principalmente, em problemas que cabem completamente em memória principal (RAM). No caso de grandes bancos de dados a memória principal pode não ser suficiente para armazenar todos os nós da árvore que compõe o índice. Por isso, é comum armazenar a estrutura de árvore (ou índice) em disco.​ Nesse caso, devemos utilizar uma representação que procure minimizar o acesso a disco para recuperação dos elementos da árvore.

A Figura 2.36 ilustra o esquema da estrutura de uma Árvore-B, que é uma árvore multivias (multiway tree), isto é, uma árvore cujos os nós podem ter mais de dois descendentes.

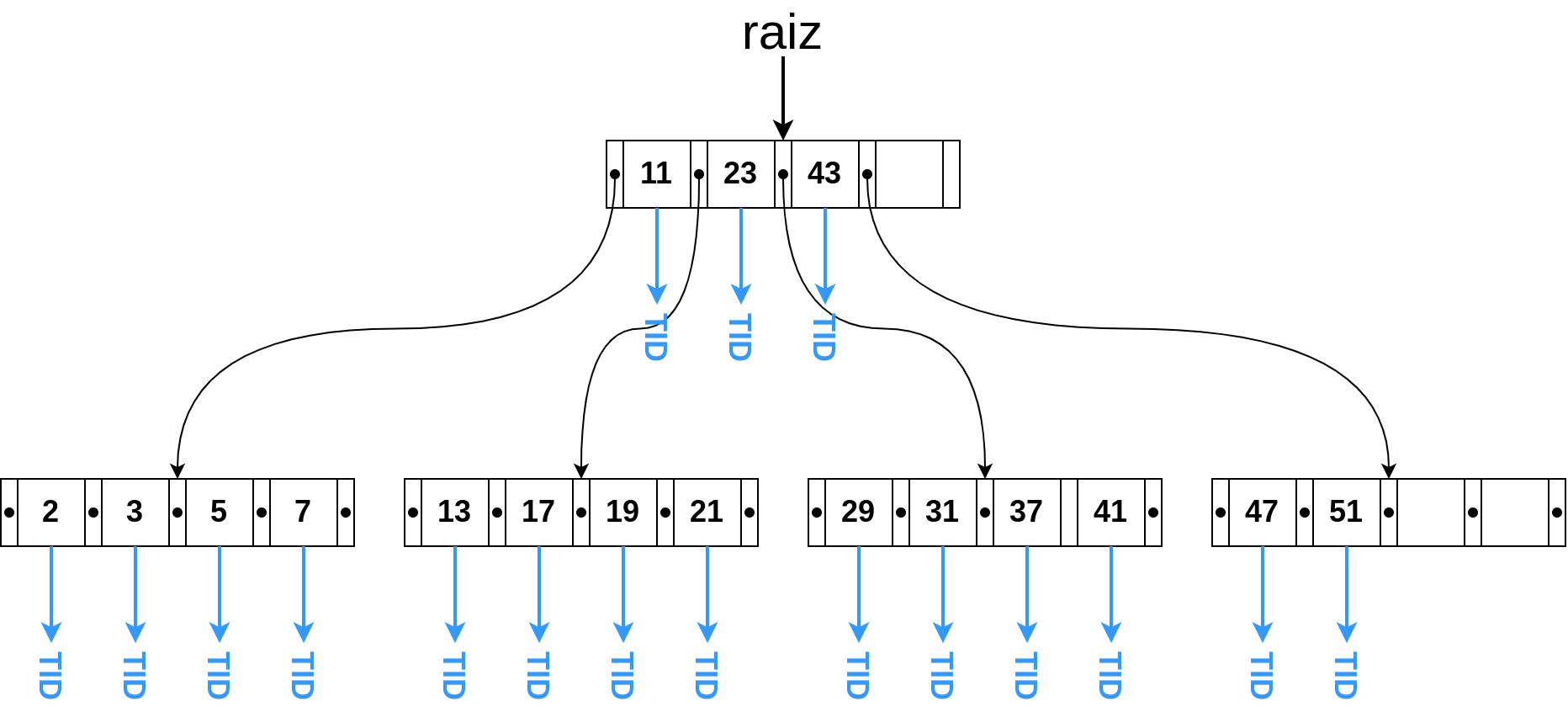
Figura 2.35 - Esquema de uma Árvore-B.

Numa Árvore-B, cada nó pode conter \(k\) descendentes e \(k - 1\) chaves, com \(m ​\leqslant k ​\leqslant M\), onde, em geral, adota-se \(m = \lceil \frac{M}{2} \rceil\). O fator \(M\) é conhecido como ordem da árvore ou fator de ramificação (branch factor ou fanout). Apenas o nó raiz pode conter um número menor do que \(m - 1\) chaves. Se a árvore possuir mais de um nível de profundidade, a raiz deve ter pelo menos 2 filhos. Todas as folhas da árvore estão no mesmo nível, isto é, trata-se de uma árvore balanceada. As chaves em cada nó devem encontrar-se em ordem crescente (ou decrescente), para permitir o uso de pesquisa binária nos valores armazendados no nó.

Os nós também são conhecidos como páginas pois comportam várias chaves além de valores que permitem estabelecer as ligações entre as páginas. Chamaremos de ponteiros os valores que permitem estabelecer as ligações entre os nós (arcos pretos). Também podemos ter associado a cada chave algum dado que ajude a localizar o objeto indexado. No nosso exemplo, estamos considerando que o índice fornece o endereço da linha associada à chave e, por isso, utilizamos o termo TID (tuple identifier) para indicar a informação de um indentificador da linha referenciada pelo índice no respectivo valor de chave.

Nos nós internos, o i-th ponteiro leva à sub-árvore com valores inferiores à i-th chave, com \(1 \leqslant i ​\leqslant M\). O último ponteiro em cada nó interno leva à sub-árvore com valores maiores ao último valor de chave nessa página. Por exemplo, o círculo preto com o arco saindo à esquerda da chave de valor 11 no nó raiz, é um ponteiro para a raiz da sub-árvore contendo todos os valores menores do que 11. De maneira similar, o círculo preto com o arco saindo à esquerda da chave de valor 23 no na raiz, é um ponteiro para a sub-árvore contendo todos os valores maiores do que 11 e menores que 23. Desta forma, cada uma das chaves ajuda a definir um intervalo de valores indexados que podem ser encontrados nas sub-árvores.

Para exemplificar o uso dessa estrutura na localização de uma chave, vamos considerar uma busca pela chave de valor 41. Partindo do nó raiz, verificamos que a chave procurada é maior que 23 e menor que 43. Nesse caso, tomamos a direção da sub-árvore indicada pelo ponteiro à esquerda do valor 43, chegando à página com as chaves \(\{29, 31, 37, 41\}\). Como essa página é uma folha e ela contém a chave procurada, podemos reportar o identificador da linha associada à chave 41.

Uma Árvore-B será mais profunda (ou terá a maior altura) quando todo nó possuir o menor fator de ramificação, isto é, quando \(m = \lceil \frac{M}{2} \rceil\). Neste caso, teríamos em cada página a seguinte quantidade de chaves:

\[\begin{split}\text{nível 0: } 1\text{ chave}\\ \text{nível 1: } 2(m-1)\text{ chaves}\\ \text{nível 2: } 2m(m-1)\text{ chaves}\\ \text{nível 3: } 2m^2(m-1)\text{ chaves}\\ \dots\\ \text{nível h: } 2m^{h-1}(m-1)\text{ chaves}\\\end{split}\]

Nota

Note que aqui estamos adotando a altura como o número de arestas no caminho mais comprido da raiz até a folha.

Nota

Podemos ler a sequência acima da seguinte forma:

• No nível 0, teremos uma \(1\) chave e, logo essa página dará origem a outras duas páginas no próximo nível (nível 1), cada uma com \(m-1\) chaves.

• No nível 1, cada uma das páginas vai dar origem a outras \(m\) páginas, de forma que teremos \(2m\) páginas no próximo nível (nível 2), cada um com \(m-1\) chaves.

• e assim, sucessivamente até o último nível da árvore denominado \(h\) (altura da árvore).​

Somando todas as chaves, teremos:​

\[\begin{split}1 + 2(m-1) + 2m(m-1) + 2m^2(m-1) + \dots + 2m^{h-1}(m-1)\\ 1 + 2(m-1)(1 + m + m^2 + \dots + m^{h-1})\\ 1 + 2(m-1)(m^0 + m^1 + m^2 + \dots + m^{h-1})\\ 1 + 2(m-1) \sum_{i=0}^{h-1} m^i = 1 + 2(m-1) \left( \frac{1-m^h}{1-m} \right) = 2m^h - 1\end{split}\]

Isso significa que o número de chaves \(n\) será: \(n \geq 2m^h-1\), ou seja:

\[\frac{n+1}{2} \geq m^h\]

\[\log_m \left( \frac{n+1}{2} \right) \geq \log_m m^h\]

\[\therefore h \leqslant \log_m \left( \frac{n+1}{2} \right)\]

A partir dessa equação, podemos assumir que para uma Árvore-B de ordem \(M = 200\), onde iremos manipular \(2.000.000\) chaves, se tomarmos \(m = 100\), teremos: \(h \leqslant 3\). Portanto, encontrar uma chave nessa árvore exige, no pior caso, avaliarmos chaves em 4 páginas.​

Podemos, portanto, concluir que para \(M\) suficientemente grande, \(h\) será pequeno, mesmo que exista um grande número de chaves na árvore. Obviamente, que deve existir um balanceamento da ordem da árvore com a capacidade de uma página do disco, que é a unidade manipulada nas operações de leitura e gravação em disco.​ O PostgreSQL, por exemplo, utiliza por padrão blocos de 8.192 bytes (ou 8 kB). Se adotarmos que as chaves sejam formadas por um número inteiro de 4 bytes e que os ponteiros de ligação entre as páginas sejam formados por inteiros de 4 bytes, uma página de 8.192 bytes seria capaz de comportar páginas de uma Árvore-B de ordem \(M = 1024\), isto é, cada página seria capaz de ramificar em até 1024 descendentes e comportar 1023 chaves (números inteiros de 4 bytes). Obviamente que aqui estamos desconsiderando o espaço necessário para representar o dado de associação com a linha tabela.

Dica

Na Internet encontram-se disponíveis vários visualizadores online capazes de demonstrar a criação de Árvores-B. O site de David Galles apresenta um visualizador interativo bastante interessante para Árvores-B.

2.23.2.4. Árvores-B⁺

A estrutura de Árvore-B apresentada na seção anterior fornece a capacidade de realizar operações de busca, inserção e remoção em tempo logarítmico, uma vez que \(h \leqslant \log_m \left( \frac{n+1}{2} \right)\). Portanto, essa estrutura fornece a capacidade de uma acesso aleatório a um dado item com muita eficiência. No entanto, os sistemas de bancos de dados devem fornecer a capacidade de recuperar registros com padrões de acesso que misturam o acesso aleatório com o sequencial. Isto ocorre quando uma busca envolve um intervalo de valores. Nesse caso, usar uma Árvore-B como a da seção anterior, poderá fazer com que seja necessária uma travessia por vários nós internos para recuperar todas as chaves dentro do intervalo pesquisado.

Existem diversas variantes da estrutura de Árvore-B apresentada na seção anterior, cada uma projetada para responder algum padrão de acesso ou utilizar uma estrutura mais adequada a certos conjuntos de dados e operações. A forma mais comum, e mais largamente empregada pelos SGBDs atuais, tanto os baseados em software livre quanto os comerciais, é a representação do índice através de uma Árvore-B⁺.​ A Figura 2.36 ilustra o esquema da estrutura de uma Árvore-B⁺.

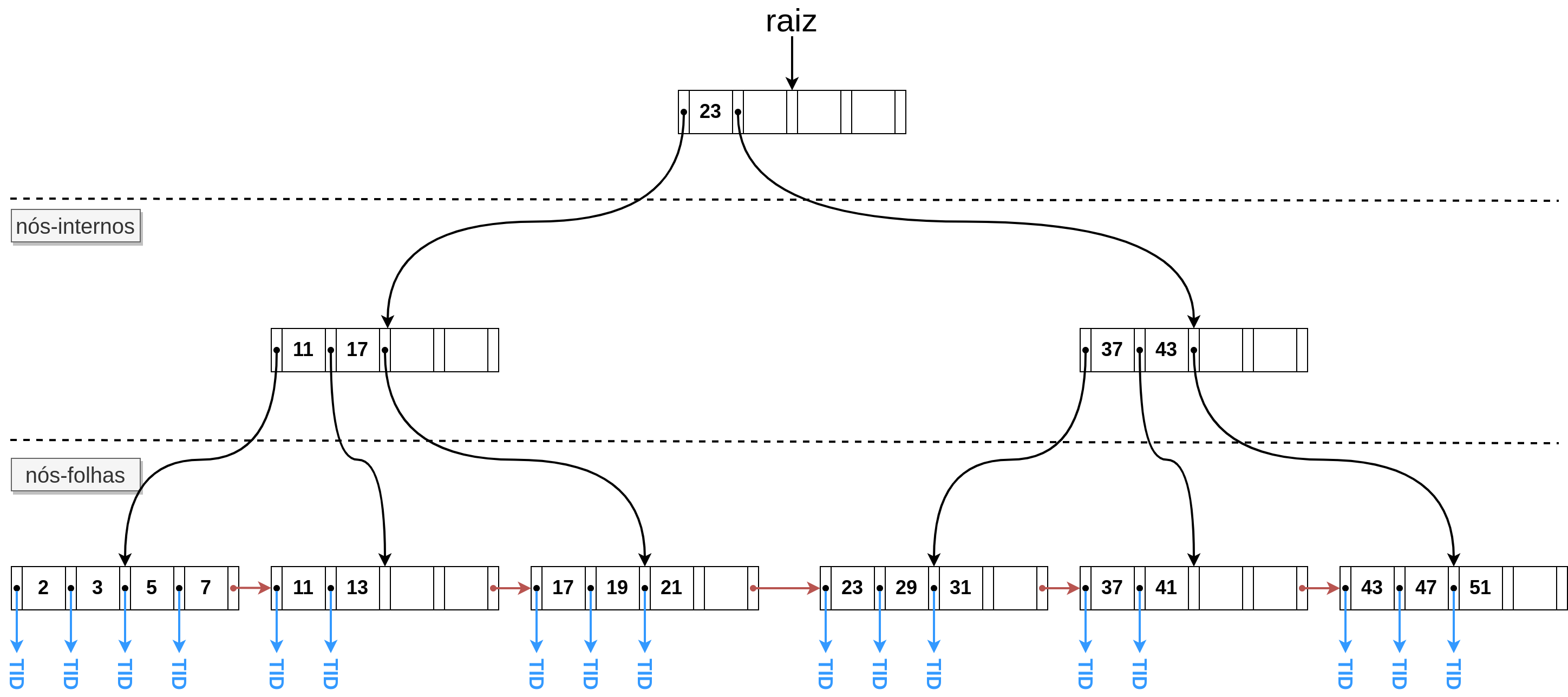
Figura 2.36 - Esquema de uma Árvore-B⁺.

A estrutura dessa árvore é muito semelhante à da Árvore-B mostrada na seção anterior, com a diferença de que nessa estrutura, todas as chaves encontram-se nas folhas e algumas chaves são usadas como guias dos nós internos​.

Nos nós internos, o i-th ponteiro leva à sub-árvore com valores inferiores à i-th chave, com \(1 \leqslant i ​\leqslant M\). O último ponteiro em cada nó interno leva à sub-árvore com valores maiores ou iguais ao último valor de chave nessa página. Por exemplo, o círculo preto com o arco saindo à esquerda da chave de valor 23 no nó raiz, é um ponteiro para a raiz da sub-árvore contendo todos os valores menores do que 23. De maneira similar, o círculo preto com o arco saindo à esquerda da chave de valor 43 no nó interno, é um ponteiro para a sub-árvore contendo todos os valores maiores ou iguais a 37 e menores que 43. Desta forma, cada uma das chaves ajuda a definir um intervalo de valores indexados pelas sub-árvores.

A estrutura das páginas dos nós folhas possui, além das chaves, ponteiros para os objetos indexados relacionados ao valor de chave. Esse valor é indicado pelos arcos azuis. No nosso exemplo, estamos considerando que o índice fornece o endereço da linha associada à chave e, por isso, utilizamos o termo TID (tuple identifier) para indicar a informação de um indentificador da linha referenciada pelo índice no respectivo valor de chave. Outra diferença dessa estrutura é que o último elemento das páginas dos nós folhas possui uma ligação para a página contendo os valores de chave na sequência, indicado na figura por uma seta em vermelho. Essa ligação entre as páginas no nível das folhas pemite utilizar o índice da Árvore-B⁺ para recuperação de intervalos.

Para exemplificar o uso dessa estrutura na localização de um objeto indexado por ela, vamos considerar uma busca pela chave de valor 41. Partindo do nó raiz, verificamos que a chave procurada é maior que a única chave presente nesse nó, que é 23. Nesse caso, tomamos a direção da sub-árvore com valores maiores ou iguais a 23, chegando à página com as chaves \(\{37, 43\}\). Como a chave procurada é maior ou igual a 37 e menor que 43, seguimos a ligação para página contendo as chaves \(\{37, 41\}\). Como essa página é uma folha e ela contém a chave procurada, podemos reportar o identificador da linha associada à chave 41.

Essa estrutura ainda permite responder consultas de intervalos unidimensionais. Considere a busca pelas linhas com chaves de valores maiores que 29 e menores que 43. Assim como no exemplo anterior, a busca é iniciada pelo nó raiz. Como o menor valor do intervalo procurado é maior ou igual à chave na raiz, tomamos o caminho da página com as chaves \(\{37, 41\}\). Como a chave procurada é menor do que a chave 37, seguimos o caminho da página na folha da árvore contendo as chaves \(\{23, 29, 31\}\). A partir dessa página, podemos varrer sequencialmente as páginas no nível das folhas até encontrar um valor de chave maior ou igual a 43. As ligações entre as páginas no nível da folha, mostradas em vermelho, possibilitam esse acesso sequencial de maneira eficiente.

Nota

As Árvores-B assim como algumas de suas variantes foram introduzidas em 1972 por Bayer e Mccreight [3]. Uma boa revisão da literatura sobre sobre Árvores-B e suas variantes pode ser encontrada em [11].

Dica

Na Internet encontram-se disponíveis vários visualizadores online capazes de demonstrar a criação de Árvores-B⁺. O site de David Galles apresenta um visualizador interativo bastante interessante para Árvores-B.

2.23.3. Indexação no PostgreSQL

O PostgreSQL fornece diversos mecanismos para indexação. O emprego de cada um deles depende do tipo de dado e das operações desejadas nas consultas. Os mecanismos fornecidos são:

• B-Tree: Pode ser empregado nas consultas que envolvem comparações de igualdade ou de intervalo unidimensional. Quando uma coluna é indexada com este tipo de índice e ela aparece na consulta junto com um dos operadores <, <=, =, >= ou >, o query planner do PostgreSQL irá considerar o uso do índice no processamento da consulta.

• Hash: É usado para indexar conjuntos de dados que são pesquisados apenas pela igualdade. Logo, quando uma coluna é indexada com este tipo de índice e ela aparece na consulta junto com o operador =, o query planner do PostgreSQL irá considerar o uso do índice no processamento da consulta. A aplicação desse tipo de índice é muito específica e, geralmente, pouco utilizado na prática, principalmente pelo fato de suportar apenas um tipo de consulta: por igualdade de chave.

• GiST (Generalized Search Tree): Trata-se na verdade de um framework para criação de índices [19]. É uma peça fundamental nos componentes de extensibilidade do PostgreSQL para possibilitar a criação de tipos de dados mais complexos que possam ser indexados. A extensão geoespacial PostGIS, que iremos abordar mais adiante, fornece tipos geométricos e matriciais com suporte a indexação espacial do tipo R-Tree. Cada implementação de índice baseada no GiST fornece seu conjunto de operadores de indexação. Por exemplo, colunas baseadas nos tipos geométricos do PostGIS, quando indexadas com a R-tree bi-dimensional definida sobre o GiST, ao serem usadas em consultas envolvendo restrições com os seguintes operadores: <<, &<, &&, &>, >>, ~=, ~, @, &<|, <<|, |>> e |&>, faz com que o query planner considere o uso desses índices no processamento das consultas.

• SP-GiST (Space-Partitioned GiST): Assim com o mecanismo GiST, fornece um framework para criação de índices baseados em técnicas de partição espacial, como quad-trees e k-d trees [2], [14]. Voltaremos a discutir mais sobre esse tipo de índice quando falarmos de indexação espacial.

• GIN (Generalized Inverted Indexes): Usado em dados como os documentos JSON e os tipos array do PostgreSQL. Voltaremos a discutir mais sobre esse tipo de índice ao falarmos sobre o tipo jsonb do PostgreSQL.

• BRIN (Block Range Indexes): Esse tipo de índice é baseado na estratégia de ter resumos sobre os valores armazenados em intervalos de blocos físicos consecutivos de uma tabela. Daremos mais detalhes sobre esse método mais adiante.

2.23.3.1. Criação de Índices

Quando definimos que uma coluna é chave primária, automaticamente o PostgreSQL realiza a criação de um índice, geralmente, baseado em uma B-Tree, para a coluna em questão. Na tabela municipio podemos ver que existe um índice denominado municipio_pkey:

bdgeo=# \d municipio_pkey

Saída:

       Index "public.municipio_pkey"
 Column |     Type     | Key? | Definition
--------+--------------+------+------------
 id     | character(7) | yes  | id
primary key, btree, for table "public.municipio"

A sintaxe básica para criação de índices é a seguinte:

CREATE [UNIQUE] INDEX [CONCURRENTLY] nome-indice

    ON nome-tabela [USING nome-método]​

    ( {nome-coluna|(expressão)} [opclass] [ASC|DESC]​ [NULLS {FIRST|LAST}] [, ...] )​

    [ INCLUDE ( nome-coluna [, ...] ) ]

    [ WITH (storage_parameter [= value] [, ...]) ]​

    [ TABLESPACE tablespace ]​

    [ WHERE predicado ]

Vamos criar um índice na tabela municipio sobre a coluna nome:

CREATE INDEX municipio_nome_idx ON municipio (nome);

Em seguida, vamos atualizar as estatísticas sobre a tabela municipio:

ANALYZE municipio;

Agora, vamos verificar novamente como a consulta à tabela municipio envolvendo um predicado usando a coluna nome é executada:

EXPLAIN (ANALYZE TRUE)
    SELECT * FROM municipio WHERE nome = 'Araxá';

Saída:

                                                          QUERY PLAN
-------------------------------------------------------------------------------------------------------------------------------
 Index Scan using municipio_nome_idx on municipio  (cost=0.28..8.30 rows=1 width=21) (actual time=0.073..0.076 rows=1 loops=1)
   Index Cond: ((nome)::text = 'Araxá'::text)
 Planning Time: 0.446 ms
 Execution Time: 0.108 ms

Repare que agora, o PostgreSQL utiliza um acesso indexado através do novo índice municipio_nome_idx, que fornece um custo menor de execução do que a versão com busca sequencial.

2.23.3.2. Remoção de Índices

Um índice pode ser removido através do comado DROP INDEX, que possui a seguinte sintaxe:

DROP INDEX nome-indice;

2.23.3.3. Considerações Sobre Criação e Uso de Índices

Os índices são essenciais para que o SGBD forneça o mecanismo de restrição de chave primária. Isso é tão forte, que no PostgreSQL ao definir uma ou mais colunas como chave primária, um índice é automaticamente criado. O nome desse índice é dado automaticamente pelo PostgreSQL e segue o seguinte padrão: <nome-tabela>_pkey.

A restrição de chave única (UNIQUE) também é implementada com o uso de um índice que garanta que os valores de chave não sejam duplicados. O nome desse índice, quando dado automaticamente pelo PostgreSQL, segue o seguinte padrão: <nome-tabela>_<nome-coluna>[_<nome-coluna>]_key. Considere a tabela professor, um índice de chave única poderia ser criado sobre a coluna nome da seguinte forma:

CREATE UNIQUE INDEX professor_nome_key ON professor (nome);

A criação de um índice sobre uma ou mais colunas em uma tabela com dezenas de milhares de registros é uma operação relativamente rápida. Para tabelas com milhões de linhas, esse tempo pode ser um pouco maior e depende do tipo de índice a ser criado (B-tree ou GiST R-tree). Além disso, pode ser necessário alterar o parâmetro de configuração maintenance_work_mem do servidor PostgreSQL, para aumentar a quantidade de memória usada durante as operações de criação de índices, e assim acelerar a sua criação.

Índices podem ser construídos e removidos a qualquer momento.​ Uma vez criado o índice, não é necessário mais intervenções pois ele é atualizado toda vez que a tabela é modificada.​ Os índices são automaticamente atualizados durante as operações de inserção, atualização e remoção das linhas, de maneira que sua estrutura não se degrada com o tempo.

Além das consultas, um índice pode acelerar as operações de atualização e remoção de linhas quando estas estejam utilizando um predicado na cláusula WHERE que possa se beneficiar dessa indexação.

É muito comum ter tabelas com vários índices definidos sobre os campos mais utilizados em pesquisas. Apesar de ser possível a criação de diversos índices em uma mesma tabela, devemos tomar cuidado para que o excesso de índices não degrade o desempenho do sistema. Ou seja, a criação de índices deve ser feita apenas se estritamente necessária pois a manutenção da estrutura do índice acarreta em mais operações para o SGBD, podendo ter impacto direto nas operações de inserção, atualização e remoção de linhas, além de ocupar um espaço extra de armazenamento em disco. Por isso, devemos evitar a criação de índices que não sejam usados em consultas ou comandos de atualização mais frequentes.

Um índice pode ser criado sobre várias colunas. Chamamos este tipo de índice de índice multicoluna (multicolumn index). Na tabela estudante_disciplina, o índice definido pela chave primária, nomeado estudante_disciplina_pkey, é formado pelos valores dos campos matricula e codigo, como mostrado abaixo:

Saída:

Index "public.estudante_disciplina_pkey"
  Column   |  Type   | Key? | Definition
-----------+---------+------+------------
 matricula | integer | yes  | matricula
 codigo    | integer | yes  | codigo
primary key, btree, for table "public.estudante_disciplina"

Nota

Esse tipo de índice é útil quando as consultas utilizam o campo matricula, isto é, o primeiro campo das chaves do índice. Faremos um exercício com índices multicoluna na Seção 2.23.5 - Exercícios.

Nota

Os comandos e operações que podem se beneficiar da existência de um índice são:​

• SELECT, INSERT, UPDATE, DELETE

• ORDER BY

• LIMIT

• Junção de tabelas​

Nota

Um índice tipo B-tree será considerado pelo query planner quando a coluna(s) indexada(s) envolver(em) comparações usando os seguintes operadores: <, <=, =, >=, >, BETWEEN, IN e LIKE. No caso do LIKE, os índice são usados apenas se o carácter curinga estiver no fim do padrão procurado.​

2.23.3.4. Índices sobre Expressões ou Índices Funcionais

Muitas vezes realizamos consultas que envolvem a aplicação de uma expressão sobre um dos campos da tabela, como por exemplo:

SELECT * FROM municipio WHERE lower(nome) = 'araxá';

Nesta consulta aquele índice definido sobre a coluna nome da tabela municipio não será usado, como indicado abaixo:

EXPLAIN (ANALYZE TRUE) SELECT * FROM municipio WHERE lower(nome) = 'araxá';

Saída:

                                              QUERY PLAN
-------------------------------------------------------------------------------------------------------
 Seq Scan on municipio  (cost=0.00..119.55 rows=28 width=21) (actual time=3.015..7.202 rows=1 loops=1)
   Filter: (lower((nome)::text) = 'araxá'::text)
   Rows Removed by Filter: 5569
 Planning Time: 0.100 ms
 Execution Time: 7.228 ms

O fato de usarmos uma expressão como lower(nome) fará com que os valores usados para criação do índice não possam ser diretamente utilizados. Desta forma, o PostgreSQL fornece um mecanismo denominado de índices sobre expressões ou índices funcionais​. Se sempre formos usar a função lower nas consultas, então deveríamos ter criado o índice com a seguinte definição:

CREATE INDEX municipio_lower_nome_idx ON municipio ( lower(nome) );​

2.23.4. Verificando o Plano de Execução de uma Consulta no PostgreSQL

Um dos recursos de um bom SGBD é um componente denominado query planner, que é capaz de traçar vários planos de execução para uma consulta e escolher o melhor deles. Um plano de execução é representado por uma estrutura de dados do tipo árvore onde cada nó representa uma etapa do processamento da consulta. Desta forma, em uma plano é possível ter nós que representam tipos de buscas (sequenciais ou indexadas), etapas de ordenação, junção entre tabelas, agregação de valores, entre outros.

Como vimos no início deste captítulo, o comando EXPLAIN mostra o plano que será usado pelo PostgreSQL para realizar uma consulta. Sua sintaxe é a seguinte:

EXPLAIN [ ( opção [, ...] ) ] comando-sql

onde, opção pode ser um dos seguintes parâmetros: ANALYZE, BUFFERS, COSTS, FORMAT, SETTINGS, SUMMARY, TIMING, VERBOSE, WAL. Com exceção do parâmetro FORMAT, todos demais podem ser definidos com os valores lógicos TRUE ou FALSE. No caso do parâmetro FORMAT, é possível escolher um valor entre: TEXT, XML, JSON ou YAML.

A saída do comando EXPLAIN descreve a árvore do plano de execução da consulta, de maneira a fornecer informações como:​

• Tipo do nó do plano.

• Estimativa do custo inicial (ex: etapa de ordenação) e total​, ambos medidos em relação ao custo de recuperação de uma unidade do disco.

• Estimativa do número total de linhas na saída​.

• Estimativa média do tamanho (em bytes) de uma linha da saída​.

Para compreender melhor esse comando, vamos retomar o exemplo do início deste capítulo, com a seguinte consulta na tabela municipio:

SELECT * FROM municipio WHERE nome = 'Araxá';

O comando EXPLAIN sem a opção ANALYZE, simplesmente apresenta uma estimativa da execução da consulta:

EXPLAIN SELECT * FROM municipio WHERE nome = 'Araxá';

Saída:

                         QUERY PLAN
------------------------------------------------------------
 Seq Scan on municipio  (cost=0.00..105.62 rows=1 width=21)
   Filter: ((nome)::text = 'Araxá'::text)

A saída acima mostra que o PostgreSQL irá realizar uma pesquisa sequencial (Seq Scan) pelas linhas da tabela municipio, sendo estimada apenas uma linha como resultado (rows=1). Esse comando apresenta dois custos estimados (cost), o primeiro, indica o custo para iniciar a consulta (0.00) e o segundo, o custo total (105.62). ​Esse custo é medido em relação à recuperação de uma unidade do disco. Para saber o número de páginas e o número de linhas da tabela municipio, podemos consultar a tabela do catálogo do sistema chamada pg_class:

SELECT relpages, reltuples FROM pg_class WHERE relname = 'municipio';

Saída:

 relpages | reltuples
----------+-----------
       36 |      5570
(1 row)

A saída acima indica que a tabela municipio econtra-se armazenada em 36 páginas do disco e possui 5.570 tuplas ou linhas. O custo total de 105.62 para execução da consulta pode ser deduzido considerando que o plano implica em recuperar as 36 páginas do disco, irá extrair as 5.570 linhas e irá aplicar o filtro de comparação uma vez em cada linha. Logo, podemos considerar a seguinte fórmula para esse plano:

\[\begin{split}(\text{páginas disco lidas} \times \text{seq_page_cost}) + (\text{linhas analisadas} \times \text{cpu_tuple_cost}) + \\ (\text{número linhas aplicada o filtro} \times \text{cpu_operator_cost})\end{split}\]

Onde:

• seq_page_cost: Custo estimado de buscar uma página do disco. Por padrão é definido como 1.0. No caso da tabela municipio, uma busca sequencial irá recuperar 36 páginas, como mostrado na consulta acima.

• cpu_tuple_cost: Custo estimado de processar cada linha durante a consulta. Por padrão é definido como 0.01. Como a tabela possui 5.570 linhas, o custo unitário de cpu_tuple_cost será multiplicado pelo número de linhas.

• cpu_operator_cost: Custo estimado de cada chamada de operador ou função envolvidos na consulta durante sua execução. Por padrão é definido como 0.0025. Na consulta em análise, esse custo está associado ao filtro da cláusula WHERE mostrado como Filter: ((nome)::text = 'Araxá'::text) na saída do comando EXPLAIN.

Substituindo as constantes com seus valores default e o número de páginas e linhas processados, temos: \((36 \times 1.0) + (5570 \times 0.01) + (5570 \times 0.0025) = 105.62\).

Para obter a estatística do tempo de execução, podemos adicionar a opção ANALYZE ao comando acima:

EXPLAIN (ANALYZE TRUE)
    SELECT * FROM municipio WHERE nome = 'Araxá';

Saída:

                                              QUERY PLAN
------------------------------------------------------------------------------------------------------
 Seq Scan on municipio  (cost=0.00..105.62 rows=1 width=21) (actual time=0.801..1.773 rows=1 loops=1)
   Filter: ((nome)::text = 'Araxá'::text)
   Rows Removed by Filter: 5569
 Planning Time: 0.179 ms
 Execution Time: 1.804 ms

A opção ANALYZE faz com que a consulta seja de fato realizada. Desta forma, o tempo inicial e total são exibidos, em milisegundos. Esse comando também mostra o número total de execuções do nó do plano (loops). Além disso, essa saída apresenta o número de linhas descartadas após a aplicação do filtro (5569).

Se existir um índice na tabela municipio associado à coluna nome, o PostgreSQL poderá gerar um plano de execução diferente para essa consulta:

EXPLAIN (ANALYZE TRUE)
    SELECT * FROM municipio WHERE nome = 'Araxá';

Saída:

                                                          QUERY PLAN
-------------------------------------------------------------------------------------------------------------------------------
 Index Scan using municipio_nome_idx on municipio  (cost=0.28..8.30 rows=1 width=21) (actual time=0.073..0.076 rows=1 loops=1)
   Index Cond: ((nome)::text = 'Araxá'::text)
 Planning Time: 0.446 ms
 Execution Time: 0.108 ms

Dessa vez, repare que o PostgreSQL utilizou uma estratégia diferente da busca sequencial, que é a busca indexada (Index Scan) utilizando o índice municipio_nome_idx. Repare que os custos envolvidos na execução dessa consulta são bem menores que a da anterior e, consequentemente, o tempo de execução também é menor.

Como último exemplo, considere a consulta abaixo, que recupera a lista de disciplinas cursadas pelo estudante de nome Claudio:

EXPLAIN (ANALYZE TRUE)
    SELECT * FROM estudante INNER JOIN estudante_disciplina USING (matricula)
                            INNER JOIN disciplina USING (codigo)
            WHERE estudante.nome = 'Claudio';

Saída:

                                                            QUERY PLAN
-----------------------------------------------------------------------------------------------------------------------------------
 Nested Loop  (cost=18.19..20.79 rows=1 width=192) (actual time=0.088..0.115 rows=1 loops=1)
   ->  Hash Join  (cost=18.04..19.96 rows=1 width=106) (actual time=0.066..0.091 rows=1 loops=1)
         Hash Cond: (estudante_disciplina.matricula = estudante.matricula)
         ->  Seq Scan on estudante_disciplina  (cost=0.00..1.73 rows=73 width=12) (actual time=0.016..0.030 rows=73 loops=1)
         ->  Hash  (cost=18.00..18.00 rows=3 width=98) (actual time=0.026..0.027 rows=1 loops=1)
               Buckets: 1024  Batches: 1  Memory Usage: 9kB
               ->  Seq Scan on estudante  (cost=0.00..18.00 rows=3 width=98) (actual time=0.014..0.022 rows=1 loops=1)
                     Filter: ((nome)::text = 'Claudio'::text)
                     Rows Removed by Filter: 36
   ->  Index Scan using disciplina_pkey on disciplina  (cost=0.15..0.83 rows=1 width=90) (actual time=0.016..0.017 rows=1 loops=1)
         Index Cond: (codigo = estudante_disciplina.codigo)
 Planning Time: 0.533 ms
 Execution Time: 0.181 ms
(13 rows)

2.23.5. Exercícios

Exercício 1. Proponha os índices a serem criados para as tabelas populacao e homicidio criados na Seção 2.22.3.

Exercício 2. Vamos criar uma tabela chamada pts com a seguinte definição:

CREATE TABLE pts
(
    id     UUID DEFAULT gen_random_uuid(),
    x      DOUBLE PRECISION,
    y      DOUBLE PRECISION,
    word   TEXT
);

Em seguida, vamos inserir um conjunto sintético de dados nessa tabela:

INSERT INTO pts (x, y, word)
                (
                    SELECT 360.0 * random() - 180.0 AS x,
                           180.0 * random() - 90.0 AS y,
                           rpad(i::text, 10) AS word
                      FROM generate_series(1, 1000000) AS i
                );

Verifique como a seguinte consulta é realizada:

EXPLAIN ANALYZE
    SELECT *
      FROM pts
     WHERE x > 1.0 AND x < 2.0
       AND y > 1.0 AND y < 2.0;

Resultado:

                                                                     QUERY PLAN
-----------------------------------------------------------------------------------------------------------------------------------------------
 Gather  (cost=1000.00..531449.00 rows=750 width=64) (actual time=675.586..4164.905 rows=425 loops=1)
   Workers Planned: 2
   Workers Launched: 2
   ->  Parallel Seq Scan on pts  (cost=0.00..530374.00 rows=312 width=64) (actual time=554.961..1543.088 rows=142 loops=3)
         Filter: ((x > '1'::double precision) AND (x < '2'::double precision) AND (y > '1'::double precision) AND (y < '2'::double precision))
         Rows Removed by Filter: 9999858
 Planning Time: 0.313 ms
 JIT:
   Functions: 6
   Options: Inlining true, Optimization true, Expressions true, Deforming true
   Timing: Generation 4.105 ms, Inlining 158.776 ms, Optimization 773.416 ms, Emission 557.021 ms, Total 1493.318 ms
 Execution Time: 4166.328 ms
(12 rows)

Agora, crie um índice formado pelas colunas x e y:

CREATE INDEX pts_x_y_idx ON pts(x, y);

Atualize as estatísticas da tabela:

ANALYZE pts;

Verifique novamente a execução da consulta:

EXPLAIN ANALYZE
    SELECT *
      FROM pts
     WHERE x > 1.0 AND x < 2.0
       AND y > 1.0 AND y < 2.0;

Resultado:

                                                                     QUERY PLAN
---------------------------------------------------------------------------------------------------------------------------------------------------
 Bitmap Heap Scan on pts  (cost=2635.91..4544.26 rows=490 width=43) (actual time=19.921..26.043 rows=425 loops=1)
   Recheck Cond: ((x > '1'::double precision) AND (x < '2'::double precision) AND (y > '1'::double precision) AND (y < '2'::double precision))
   Heap Blocks: exact=425
   ->  Bitmap Index Scan on pts_x_y_idx  (cost=0.00..2635.79 rows=490 width=0) (actual time=19.731..19.732 rows=425 loops=1)
         Index Cond: ((x > '1'::double precision) AND (x < '2'::double precision) AND (y > '1'::double precision) AND (y < '2'::double precision))
 Planning Time: 0.481 ms
 Execution Time: 26.174 ms
(7 rows)

---

Dica

Para mais detalhes sobre o suporte de índices no PostgreSQL, consulte Chapter 11. Indexes.

Dica

Para mais detalhes sobre o comando ANALYZE, consulte ANALYZE.

Dica

Para mais detalhes sobre o comando EXPLAIN, consulte EXPLAIN.

Dica

Para mais detalhes sobre o comando CREATE INDEX, consulte CREATE INDEX.

Dica

Faça uma pesquisa para saber quando um índice pode ser utilizado na ordenação do resultado de uma consulta (ORDER BY).

Dica

Procure saber sobre um recurso poderoso do PostgreSQL: Índices Parciais.